22.3. Caratteristiche dei fenomeni ondulatori#
todo
necessità di segnali coerenti (es.laser, forzanti armoniche)?
condizioni nelle quali è lecito aspettarsi la manifestazione dei seguenti fenomeni. Es. diffrazione quando un’onda incontra ostacoli di dimensioni «paragonabili» alla lunghezza d’onda della perturbazione…
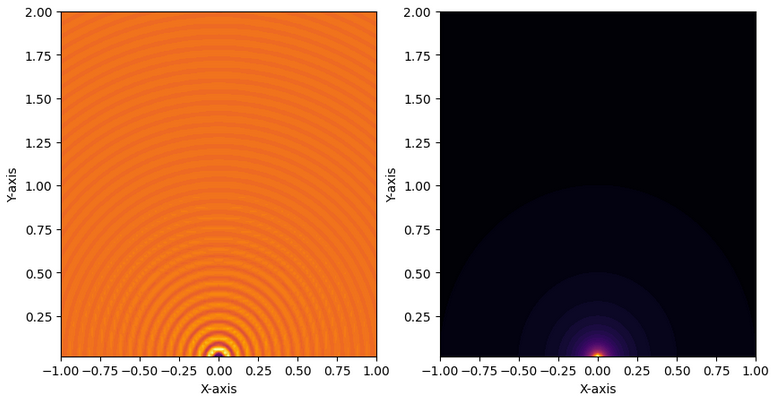
22.3.1. Interferenza#
distinguere tra PSCE di segnali, e pattern di interferenza che compare nel quadrato del segnale, spesso associato alle grandezze percepite con i sensi e/o misurate da strumenti di misura (es. intensità luminosa della radiazione elettromagnetica)
|
|
Studio sistematico della diffrazione, con esempi: di limite di Fresnel e Fraunhofer; limite di diffrazione; pattern di diffrazione in funzione della forma dell’apertura,…
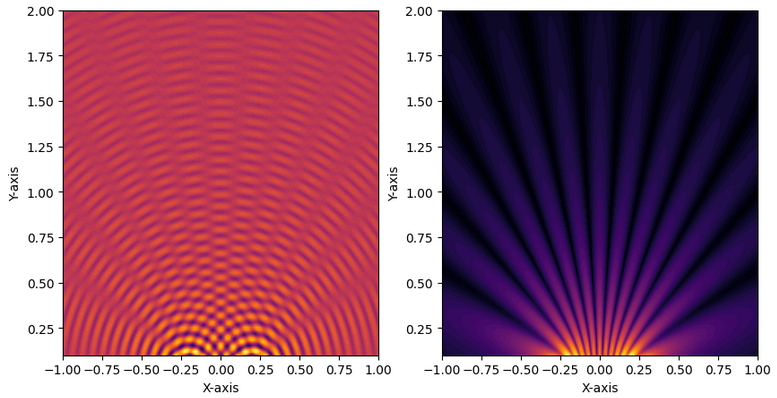
22.3.2. Diffrazione#
La diffrazione è una conseguenza dell’intereferenza di un’onda con un ostacolo o un’apertura di dimensione parabonabile alla lunghezza d’onda (Definition 22.2) della perturbazione.
Per alcune geometrie semplici, sono note alcune soluzioni approssimate dei pattern di interferenza in seguito alla diffrazione:
near-field: approssimazione di Fresnel
far-field: approssimazione di Fraunhofer
todo
Limiti di diffrazione: quando è lecito aspettarsi diosservare diffrazione?
Aggiungere esempi di soluzione esatta calcolata con script, e confronto con le approssimazioni di Fresnel e Fraunhofer; distinguere tra soprapposizione segnali, e pattern di interferenza nell’intensità media. Riferimeni: video di 3B1B - How re hologram possible?
Fare esempi pratici: lato posteriore di un DVD, doppia fenditura, reticoli di diffrazione, diaframma di una macchina fotografica con apertura ridotta,…
Applicazioni ed esempi. Spettroscopia
Example 22.4 (Doppia fenditura)
Modello: diffrazione dovuta a due fessure sufficientmente ridotte da poter essere considerate sorgenti puntiformi (in fase, o no? discutere)
Example 22.5 (Singola fenditura)
Modello: diffrazione dovuta alla sovrapposizione degli effetti di una distribuzione di sorgenti punti.
Example 22.6 (Reticolo di diffrazione)
22.3.3. Riflessione#
22.3.4. Rifrazione#
22.3.5. Polarizzazione#
Onde sismiche S, shear, di taglio
Onde EM
22.3.6. Effetto Doppler#
Quando la sorgente e l’osservatore sono in moto relativo, la frequenza percepita dall’osservatore è diversa dalla frequenza emessa dalla sorgente.
In questo paragrafo viene valutato solo l’effetto della propagazione 1-dimensionale di disturbi piani, lungo la direzione del moto relativo di sorgente e osservatore (ricevitore). Per evitare complicazioni algebriche e avere un problema risolvibile in forma chiusa senza troppe difficoltà, ci si limita al moto relativo uniforme. Le leggi del moto di sorgente e osservatore sono rispettivamente,
Il segnale emesso dalla sorgente \(A_s(t) = F \cos(\Omega_s t)\) si propaga come due onde viaggianti in direzione opposta,
con la funzione \(H(y) = 1\) per \(y = \text{True}\), \(H(y)=0\) se \(y= \text{False}\) necessaria a limitare la soluzione al dominio di influenza.
Quando l’osservatore si trova a destra della sorgente, \(x_r(t) > x_s(t)\) (todo ruolo di \(t_{ret}\), onde d’urto,…) esso è raggiunto al tempo \(t\) dalla parte di segnale che si propaga verso destra emesso nell’istante di tempo \(t^+_{ret}\)
L’osservatore registra un segnale precedente emesso dalla sorgente uguale a
quindi nel caso di segnale armonico, la pulsazione della frequenza registrata è
Quando l’osservatore si trova a sinistra della sorgente, \(x_r(t) < x_s(t)\) (todo ruolo di \(t_{ret}\), onde d’urto,…) esso è raggiunto al tempo \(t\) dalla parte di segnale che si propaga verso sinistra emesso nell’istante di tempo \(t^-_{ret}\)
L’osservatore registra un segnale precedente emesso dalla sorgente uguale a
quindi nel caso di segnale armonico, la pulsazione della frequenza registrata è
Example 22.7 (Stima della velocità dell’ambulanza con effetto Doppler)
Si conosce la temperatura ambiente, \(T_a\), che permette di valutare la velocità di propagazione del suono, \(c = \sqrt{\gamma R T}\). Mentre ci si trova per strada ad aspettare l’autobus, e stiamo giocando con il nostro smartphone con un’app che rende disponibili la misura della frequenza dei suoni ricevuti, sentiamo arrivare un’ambulanza.
Essendo a conoscenza dell’effetto Doppler, vogliamo stimare la velocità dell’ambulanza osservando la frequenza misurata del suono emesso dalla sirena dell’ambulanza mentre si sta avvicinando \(f_1\) e mentre si sta allontanando da noi \(f_2\). Si chiede quindi di:
stimare la velocità dell’ambulanza, \(v\), rispetto alla strada
stimare la frequenza della sorgente, \(f_0\)
una volta nota la velocità dell’ambulanza e la frequenza del segnale emesso calcolati ai punti 1. e 2., stimare le frequenze misurate nei casi in cui:
non fossimo fermi rispetto alla strada, ma ci stessimo muovendo a un passo di \(v_r = 1 \, m/s\) nella stessa direzione dell’ambulanza
fossimo fermi rispetto alla strada, ma ci fosse un vento uniforme con velocità \(v_m = 3 \, m /s\) che soffia nella stessa direzione del moto dell’ambulanza
Soluzione
(1-2) Supponiamo che l’ambulanza si muova da sinistra verso destra.
Ambulanza in avvicinamento. Mentre l’ambulanza si avvicina a noi, veniamo raggiunti dalla parte disegnale che viaggia verso destra, \(f(x - c t)\)…Il segnale registrato ha una frequenza data dall’espressione (22.4), con velocità dell’osservatore \(v_r = 0 \)
Ambulanza che si allontana. Mentre l’ambulanza si allontana veniano raggiunti dalla parte di segnale che si muove verso sinistra, \(f(x+ct)\)…Il segnale registrato ha una frequenza data dall’espressione (22.5), con velocità dell’osservatore \(v_r = 0 \)
Mettendo a sistema le due equazioni, si può calcolare la velocità dell’ambulanza e la frequenza della sirena
(3) …
Example 22.8 (Effetto doppler in astronomia)
Si vuole determinare velocità della galassia XXX todo analizzando la radiazione elettromagnetica emessa dalla galassia che arriva sulla Terra. Nello spettro di emissione si riconosce la linea \(H-\alpha\), legata alla presenza di idrogeno ionizzato, e a una transizione di un \(e^-\) di un atomo di \(H\) dal livello di energia \(n=3\) al livello di energia \(n=2\).
Queta riga spettrale è associata a una lunghezza d’onda \(\lambda^0_{H\alpha} = 656.46 \, nm\) nel vuoto, e quindi \(f^0_{H\alpha} = ...\), in un sistema in quiete relativa.
Nello spettro misurato si riconosce la linea \(H\alpha\) con una lunghezza d’onda \(\lambda = 659.5 \, nm\). (Virgo cluster)
Si chiede di:
calcolare la velocità radiale usando le formule per l’effetto Doppler non relativistico
valuatere l’errore commesso usando le formule dell’effetto Doppler non relativistico, rispetto all’uso delle formule che tengono conto degli effetti relativistici
Il rapporto,
viene definito red-shift, o spostamento verso il rosso, come sarà più chiaro nella discussione dello spettro elettromagnetico