10.5. Problemi#

Questa pagina contiene esercizi di statica suddivisi in quattro categorie: statica del punto materiale, sistemi di punti materiali, corpi rigidi, e una sezione varia. Gli esercizi sono progettati per studenti con una buona conoscenza della statica e delle sue applicazioni.

10.5.1. Statica del punto materiale#

Uncomment

10.5.2. Sistemi di punti materiali#

Uncomment

10.5.3. Statica del corpo rigido#

Uncomment

10.5.4. Miscellanea#

Uncomment

Problema 1.

Data la massa \(m\) della massa puntiforme appeso tramite due fili inestensibili ideali di lunghezza \(L_1\) e \(L_2\) note, si calcolino le reazioni a terra.

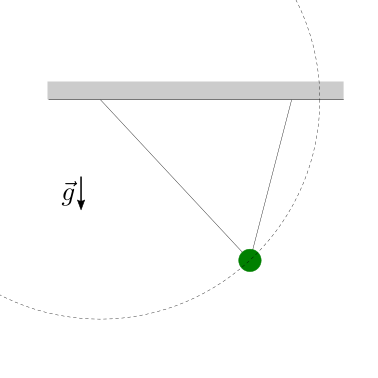
Soluzione.
Problema 2.

Data la massa \(m\) della massa puntiforme appeso tramite due fili inestensibili ideali di lunghezza \(L_1\) nota e \(L_2\) variabile, si calcolino le reazioni a terra in funzione della lunghezza del filo \(2\).

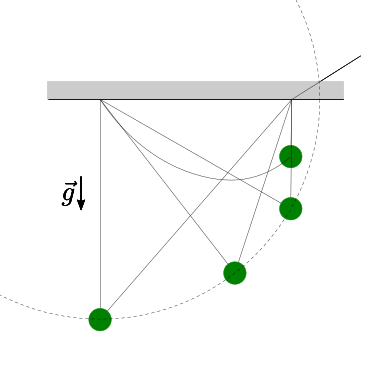
Soluzione.
Problema 3.

Data la massa \(m\) della massa puntiforme appeso tramite un filo inestensibile ideale di lunghezza \(L\) e una molla di costante elastica \(k\) e lunghezza a riposo \(x_0\) collegata a terra in un punto distante \(H\) dal punto a terra dove è collegato il filo, si calcoli:

  1. la posizione del punto

  2. la lunghezza della molla

  3. le reazioni vincolari a terra nella configurazione di equilibrio.

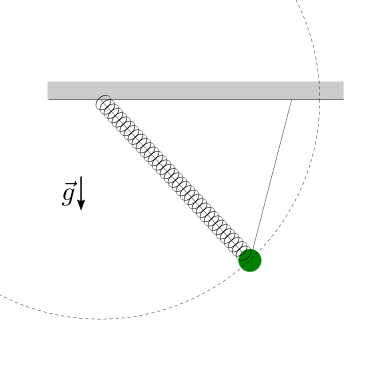
Soluzione.
Problema 4.

Data \(m\), \(\mu^s\), trovare l’angolo massimo \(\theta_{\max}\) per il quale esiste una condizione di equilibrio.

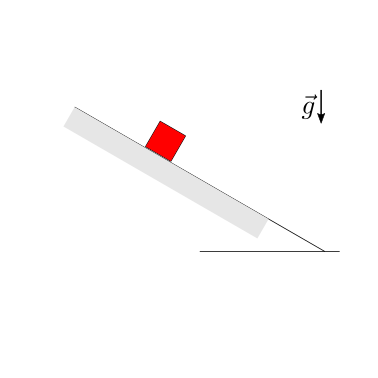
Soluzione.
Problema 5.

Data \(m\), \(M\), \(\mu^s\) tra i due solidi, si chiede di calcolare:

  • la risultante delle azioni scambiate tra i due corpi

  • la risultante delle reazioni vincolari a terra agenti sul solido blu,

nella condizione di equilibrio del sistema, nell’ipotesi che l’attrito tra solido blu e terra sia trascurabile. Verificare le condizioni limite tra \(\theta\) e \(\mu^s\) affinché l’equilibrio sia possibile

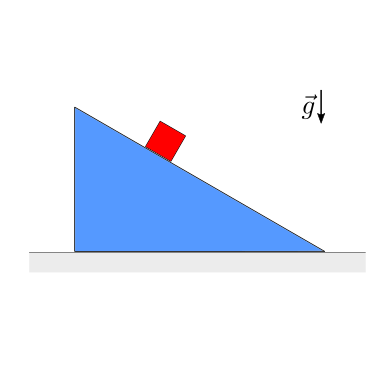
Soluzione.
Problema 6.

Data la massa \(m\) del blocco rosso, la costante elastica \(k\) della molla lineare ideale, con lunghezza a riposo \(\ell_0\), viene chiesto di:

  • determinare la lunghezza della molla nella condizione di equilibrio, nell’ipotesi che l’attrito tra blocco rosso e piano inclinato sia trascurabile

  • determinare le possibili condizioni di equilibrio, nell’ipotesi che l’attrito statico tra blocco rosso e piano inclinato sia \(\mu^s\)

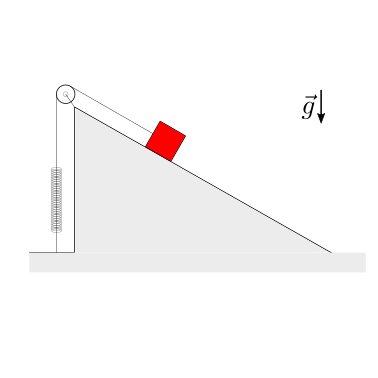
Soluzione.
Problema 7.

Data la massa \(m\) del blocco rosso, il raggio \(R_1\), \(R_2\) delle due carrucole, si chiede di determinare la forza \(\vec{F}\) da applicare nella condizione di equilibrio, nell’ipotesi di fili inestensibili e carrucole ideali e senza massa.

Si chiede poi di ripetere il calcolo nell’ipotesi in cui la massa delle carrucole non sia trascurabile, ma siano \(M_1\) per la carrucola vincolata a terra, e \(M_2\) per la carrucola non vincolata a terra.

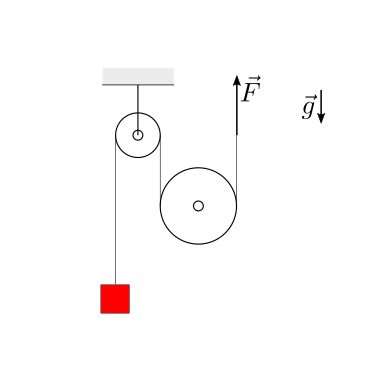
Soluzione.
Problema 8.

Nel meccanismo di un orologio i 3 componenti che devono guidare il moto delle lancette dei secondi, dei minuti e delle ore, connessi «in cascata» tramite ingranaggi (con rapporto dei raggi \(1:60\) todo scriverlo esplicitamente?). Conoscendo la costante elastica \(k\) e la compressione \(\Delta \theta\) della molla che guida il componente che guida la lancetta delle ore, si chiede di:

  • determinare la forza necessaria da applicare alla lancetta dei secondi nel punto indicato nell’imagine, necessaria a garantire la posizione di equilibrio

  • le reazioni vincolari in corrispondenza delle cerniere che collegano a terra i 3 componenti, nell’ipotesi che non si scambino forze in direzione radiale.

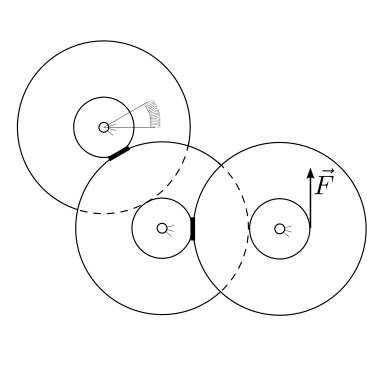
Soluzione.
Problema 9.

Data la lunghezza \(L\) e la massa \(m\) dell’asta rigida con distribuzione di massa uniforme e il coefficiente di attrito stativo \(\mu^s\) tra asta e superficie orizzontale, si chiede di:

  • determinare la condizione limite dell’equilibrio

  • determinare le reazioni a terra nell’ipotesi che l’attrito sulla superficie verticale sia trascurabile

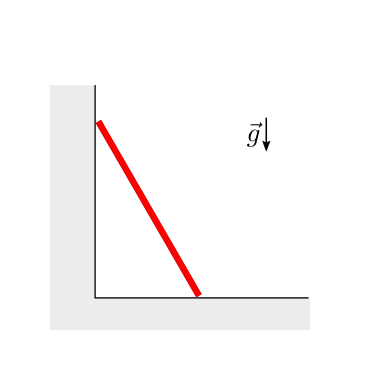
Soluzione.
Problema 10.

Data la lunghezza \(L\) e la massa \(m\) dell’asta rigida incernierata a terra, e la costante elastica \(k\) della molla rotazionale, si chiede di:

  • calcolare la condizione di equilibrio

  • le reazioni vincolari sull’asta discutendo i due casi determinati dalla condizione di appoggio dell’estremo superiore dell’asta sulla parete verticale.

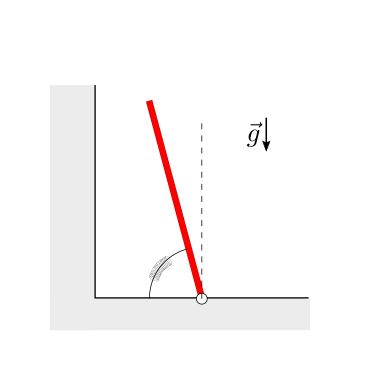
Soluzione.
Problema 11.

Testo del problema…

Soluzione.
Problema 12.

Testo del problema…

Soluzione.
Problema 13.

Testo del problema…

Soluzione.
Problema 14.

Testo del problema…

Soluzione.
Problema 15.

todo Equilibrio di un corpo appoggiato…esempio che mostra come la retta di applicazione del peso deve cadere nella base di appoggio; qui non è possibile introdurre l’accelerazione del sistema (todo aggiungere esercizio nel capitolo della dinamica), ma si può fare un esercizio con superficie di appoggio permendicolare e non al campo di gravità locale. L’unica cosa che conta è la direzione relativa tra superficie di appoggio e forza di massa. Rimandare all’esercizio sulla dinamica con collegamento

Soluzione.
Problema 16.

todo Sollevamento di un peso sbilanciato, come mostrato in un «video virale»

Soluzione.

10.5.5. Statica dei fluidi#

Problema 20.

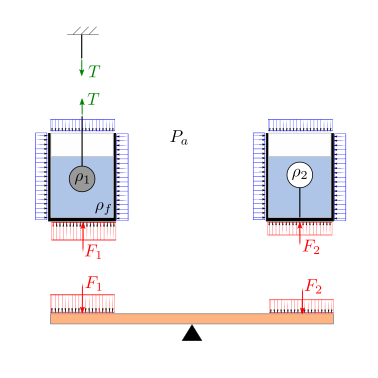
Due scatole uguali sono posizionate su una leva alla stessa distanza dal fulcro e contengono lo stesso volume \(V_f\) di acqua di densità \(\rho_f\). Nell’acqua contenuta nelle due scatole sono immerse completamente due sfere che hanno lo stesso volume \(V\) di metallo di densità \(\rho_1 > \rho_f\) e una sfera con \(\rho_2 < \rho_f\). La sfera di metallo è appesa con un filo ideale a una parete esterna, mentre la sfera 2 è ancorata al fondo della scatola. Il sistema è immerso in un campo gravitazionale uniforme, le scatole sono poste alla stessa distanza dalla cerniera della leva sulla quale sono appoggiate, con la quale scambiano solo azioni in direzione perpendicolare alla superficie. Si assuma quindi1 che la risultante delle forze di contatto abbia punto di applicazione nel centro della base.

Viene chiesto di:

  1. determinare se la bilancia si trova in una posizione di equilibrio. Se no, in quale direzione tenderà a ruotare?

  2. calcolare la tensione nel filo al quale è appesa la sfera metallica.

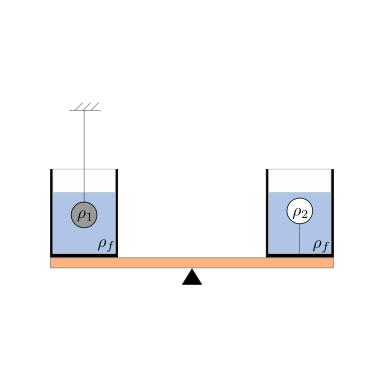
Soluzione

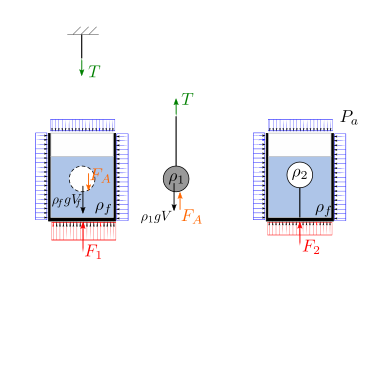
Per determinare l’equilibrio alla rotazione del sistema è necessario valutare i momenti delle forze esterne agenti su di esso. Prendendo come segno positivo dei momenti quello che fa ruotare la leva in senso anti-orario.

\[\begin{split}\begin{aligned} M^e_H & = - \rho_f V g L - \rho_2 V_2 g L - P_a S L - T L + \rho_f V g L + \rho_1 V g L + P_a S L = \\ & = - \rho_2 V g L - T L + \rho_1 V g L \ . \end{aligned}\end{split}\]

Per determinare la tensione \(T\) dell filo si usa la condizione di equilibrio per la sfera metallica. Sulla sfera agiscono la tensione del filo, il proprio peso e la forza di galleggiamento di Archimede,

\[\begin{split}\begin{aligned} 0 & = - \rho_1 V g + T + F_{Arch} = \\ & = - \rho_1 V g + T + \rho_f V g \\ T = & (\rho_1-\rho_f) V g \end{aligned}\end{split}\]

La risultante dei momenti esterni vale quindi

\[M^e_H = \left( \rho_f - \rho_1 \right) g V L < 0 \ . \]

Poiché la risultante dei momenti non è nulla, il sistema non si trova in una condizione di equilibrio. Poiché \(M^e_H < 0\) - per le convenzioni scelte sui segni, verso positivo di rotazione e momenti in senso anti-orario - il sistema tende a ruotare in senso orario

1

Se i due corpi scambiano solo reazioni in direzione perpendicolare alla parete, questa condizione è sufficiente per garantire che il punto - o meglio la retta - di applicazione della risultante delle forze si trovi nel centro della base della scatola. Ma c’è equilibrio qui?