21.1. Equazione delle onde in diversi sistemi

In questa sezione viene discusso il ruolo dell”equazione delle onde in diversi ambiti della fisica. La dinamica di perturbazioni di ampiezza «sufficientemente piccola» è descritta da un problema lineare, governato dall’equazione delle onde con le oppportune condizioni iniziali e al contorno. Per problemi in domini \(D\) spaziali \(1\)-dimensionali, l’espressione dell’equazione (lineare) delle onde in un mezzo omogeneo è

(21.1)\[\frac{1}{c^2} \partial_{tt} u - \partial_{xx} u = f(x, t) \ , \qquad x \in D \ ,\]

dove \(c\) è la velocità di propagazione delle perturbazioni. Questa velocità è una costante del problema in mezzi omogenei. Il significato della costante \(c\) come velocità di propagazione delle perturbazioni risulta chiaro nell’espressione delle onde viaggianti come soluzioni elementari dell’equazione delle onde.

Per domini \(n\)-dimensionali, l’espressione dell’equazione delle onde in un mezzo omogeneo è

\[\frac{1}{c^2} \partial_{tt} u - \nabla^2 u = f(\vec{r}, t) \ , \qquad \vec{r} \in D \ .\]

Nelle sezioni successive viene mostrato come l’equazione delle onde compare in diversi ambiti della fisica, da sistemi meccanici elastici, alle onde di pressione per l’acustica, alle onde elettromagnetiche.

21.1.1. Problemi strutturali

21.1.1.1. Azione assiale - catena di molle lineari

L’azione assiale nelle travi elastiche può essere rappresentata con un sistema discret(izzat)o di masse e molle lineari. La trave viene discretizzata con \(N+1\) masse concentrate, connesse da \(N\) molle.

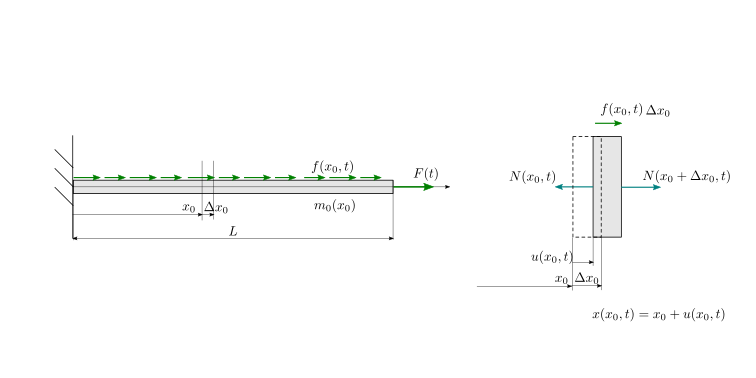
Fig. 21.1 Trave soggetta ad azione assiale. Modello continuo.

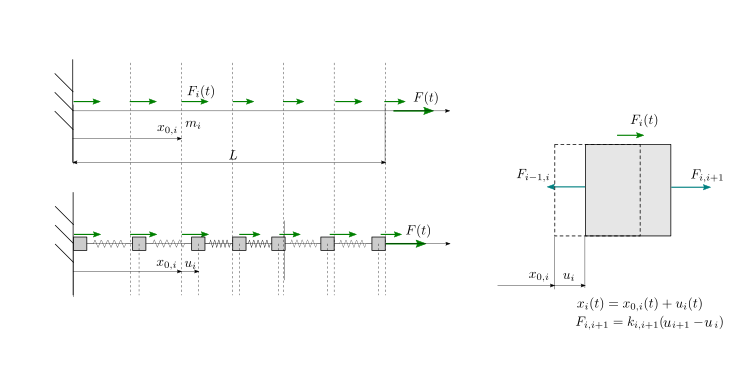
Fig. 21.2 Trave soggetta ad azione assiale. Modello discreto: la viene rappresentata come un insieme di masse concentrate connesse da molle. Il moto fuori dall’asse della trave è impedito da un vincolo di pattino, che costringe le masse a muoversi solo lungo l’asse.

La posizione di una massa è

\[X_i(t) = X_{0,i} + U_i(t) \ ,\]

cioè la somma della posizione di riferimento e lo spostamento \(U_i\). Nella configurazione di riferimento la struttura non è soggetta a sforzi, e le molle hanno allungamento nullo. Segue che l’allungamento della molla tra la massa \(i\) e \(j\) è

\[\Delta \ell_{i,i+1} = \ell_{i,i+1} - \ell_{i,i+1}^0 = X_{i+1} - X_{i} - X_{i+1}^0 + X_{i}^0 = U_{i+1} - U_{i} \ .\]

todo. Discussione sui valori delle masse concentrate e della rigidezza delle molle. Questo è determinato dall’approssimazione utilizzata. Una buona approssimazione discreta deve convergere alla soluzione del problema continuo, all’aumentare del numero di gradi di libertà del modello.

La \(i\)-esima massa è soggetta alle forze elastiche dovute alla connessione con le masse adiacenti e alla forzante esterna. Il bilancio della quantità di moto per la \(i\)-esima massa è quindi

\[\begin{split}\begin{aligned} M_i \ddot{U}_i & = F_{i,i-1} + F_{i,i+1} + F^e_i = \\ & = K_{i,i-1} \left( - U_i + U_{i-1} \right) + K_{i,i+1} \left( - U_i + U_{i+1} \right) + F^e_i \ . \end{aligned}\end{split}\]

Questa equazione è valida per ogni massa (ad eccezione delle masse agli estremi della trave, ma lì entrano in azione le condizioni al contorno). Assumendo che la distribuzione di massa e la rigidezza della trave sia uniforme,

\[M_i = m \, \Delta x \quad , \quad K = {EA}{\Delta x} \ ,\]

l’equazione per la \(i\)-esima massa diventa

\[\Delta x m \ddot{U}_i - \frac{EA}{\Delta x} \left( U_{i-1} - 2 U_i + U_{i+1} \right) = \Delta x f_i \ ,\]

e dividendo per \(\Delta x\)

\[m \ddot{U}_i - EA \frac{U_{i-1}- 2 U_i + U_{i+1}}{\Delta x^2} = f_i \ .\]

Si riconosce infine l’approssimazione del secondo ordine della derivata seconda della funzione \(u(x,t)\) valutata in \(X_i\). La si sostituisce con essa e si introduce la notazione di derivate parziali (per funzioni che dipendono da più variabili indipendenti, qui spazio \(x\) e tempo \(t\)) per trovare l’equazione delle onde

\[m \partial_{tt} u - EA \partial_{xx} u = f \ .\]

Confrontando questa espressione con l’espressione (21.1) dell’equazione delle onde, si può ricavare che la velocità di propagazione delle onde assiali è

\[c_{u} = \sqrt{\frac{EA}{m}} \ .\]

Example 21.1 (Modello discreto)

\[M_j \ddot{U}_j(t) = F_{j,j-1} + F_{j,j+1} + F_j^{ext}(t) = K_{j,j-1} \left( U_{j-1}(t) - U_j(t) \right) + K_{j,j+1} \left( U_{j+1}(t) - U_{j}(t) \right) + f_j^{ext}\]

Se le molle hanno tutte la stessa rigidezza, \(K\),

(21.2)\[M_j \ddot{U}_j(t) - K \left( U_{j-1}(t) - 2 U_j(t) + U_{j+1}(t) \right) = F^e_j(t) \ .\]

Condizioni iniziali e condizioni al contorno.

Forma matriciale. Il problema può essere riscritto usando il formalismo matriciale come

\[\begin{aligned} \mathbf{M} \ddot{\mathbf{U}} + \mathbf{K} \mathbf{U} = \mathbf{F}^e \ , \end{aligned}\]

con le matrici

\[\begin{split}\mathbf{K} = K \begin{bmatrix} 2 & -1 & 0 & 0 & 0 & \dots & 0 \\ -1 & 2 & -1 & 0 & 0 & \dots & 0 \\ 0 & -1 & 2 & -1 & 0 & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ 0 & 0 & \dots & 0 & 2 & -1 & 0 \\ 0 & 0 & \dots & 0 & -1 & 2 & -1 \\ \end{bmatrix}\end{split}\]

\[\begin{split}\mathbf{M} = \begin{bmatrix} M_1 & 0 & 0 & \dots & 0 \\ 0 & M_2 & 0 & \dots & 0 \\ 0 & 0 & M_3 & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots \\ 0 & 0 & \dots & M_{n-1} & 0 \\ 0 & 0 & \dots & 0 & M_n \\ \end{bmatrix}\end{split}\]

\[\mathbf{U}(t) = \begin{bmatrix} U_0(t) & U_1(t) & \dots & U_n(t) \end{bmatrix}^T\]

\[\mathbf{F}(t) = \begin{bmatrix} F_0(t) & F_1(t) & \dots & F_n(t) \end{bmatrix}^T\]

Approssimazione di un problema continuo. Gli elementi del vettore \(\mathbf{U}\) possono essere interpretati come i valori di una funzione del tempo e dello spazio, \(u(x,t)\), per determinati valori della variabile indipendente \(x\),

\[U_j(t) = u(x_j, t) \ .\]

Se i punti di coordinata \(x_j\) hanno intervalli regolari,

\[x_j = x_{j-1} + \Delta x \qquad , \qquad x_j = j \, \Delta x \qquad j = 0:n \ ,\]

con \(\Delta x\) «sufficientemente piccolo», allora l’approssimazione in serie di Taylor

\[\begin{split}\begin{aligned} & u(x_i,t) \\ & u(x_i+\Delta x, t) = u(x_i,t) + \Delta x \partial_x u(x_i,t) + \dfrac{1}{2} \Delta x^2 \partial_{xx} u(x_i,t) + o(\Delta x^2) \\ & u(x_i-\Delta x, t) = u(x_i,t) - \Delta x \partial_x u(x_i,t) + \dfrac{1}{2} \Delta x^2 \partial_{xx} u(x_i,t) + o(\Delta x^2) \\ \end{aligned}\end{split}\]

permette di riconoscere l’approssimazione centrata della derivata seconda \(\partial_{xx} u(x_i, t)\) valutata in \(x = x_i\),

\[\partial_{xx} u(x_i,t) = \dfrac{u(x_i-\Delta x,t) - 2 u(x_i,t) + u(x_i+\Delta x,t)}{\Delta x^2}\]

\[M_j \partial_{tt} u(x_j,t) - K \partial_{xx} u(x_j,t) = F_j(t) \]

21.1.1.2. Torsione - catena di molle rotazionali

Seguendo quanto fatto per l’azione assiale, si può ricavare l’equazione delle onde per la torsione di una trave,

\[I \partial_{tt} \theta(x,t) - GJ_t \partial_{xx} \theta(x,t) = m(x,t) \ .\]

Confrontando questa espressione con l’espressione (21.1) dell’equazione delle onde, si può ricavare che la velocità di propagazione delle onde assiali è

\[c_{t} = \sqrt{\frac{GJ_t}{I}} \ .\]

21.1.1.3. Filo teso

La dinamica trasversale di un filo teso con pre-sforzo assiale \(N_0 = A \sigma_0\) è

\[m \partial_{tt} v(x,t) - N_0 \partial_{xx} v(x,t) = f(t)\]

Confrontando questa espressione con l’espressione (21.1) dell’equazione delle onde, si può ricavare che la velocità di propagazione delle onde assiali è

\[c_{v} = \sqrt{\frac{N_0}{m}} \ .\]

Dynamical equations. Out-of-axis component of the momentum equation of the \(i\)-th mass reads

\[\begin{split}\begin{aligned} M \ddot{w}_i & = F_i^e - F_{i-1,i} \theta_{i,i-1} + F_{i,i+1} \theta_{i,i+1} = \\ & = F_i^e - F_{i-1,i} \dfrac{w_i - w_{i-1}}{\Delta x} + F_{i,i+1} \dfrac{w_{i+1}-x_{i}}{\Delta x} = \\ \end{aligned}\end{split}\]

with the approximations \(\sin \theta_{i,i+1} \sim \theta_{i,i+1} \sim \dfrac{w_{i+1}-w_i}{\Delta x}\) and \(F_{i,i+1} = N_0\) for small displacements. If \(M_i = m \Delta x\), with \(\mu\) linear mass density, and the lumped force is written as a linear force density \(F_i = \Delta x \, f_i(t)\)

\[\begin{aligned} \Delta x \, m \ddot{w}_i(t) - N_0 \dfrac{w_{i+1}(t) - 2 w_i(t) + w_{i-1}(t)}{\Delta x} = \Delta x \, f_i^e \end{aligned}\]

and dividing by \(\Delta x\), adn recognizing the center scheme for the second order partial derivative in space,

\[\begin{split}\begin{aligned} m \ddot{w}_i(t) - N_0 \dfrac{w_{i+1}(t) - 2 w_i(t) + w_{i-1}(t)}{\Delta x^2} & = \, f_i^e \\ m \partial_{tt} \ddot{w}(x,t) - N_0 \partial_{xx} w(x,t) & = \, f(x,t) \end{aligned}\end{split}\]

the wave equation for the out-of-plane dispalcement appears.

Esempio: corde di strumenti musicali.

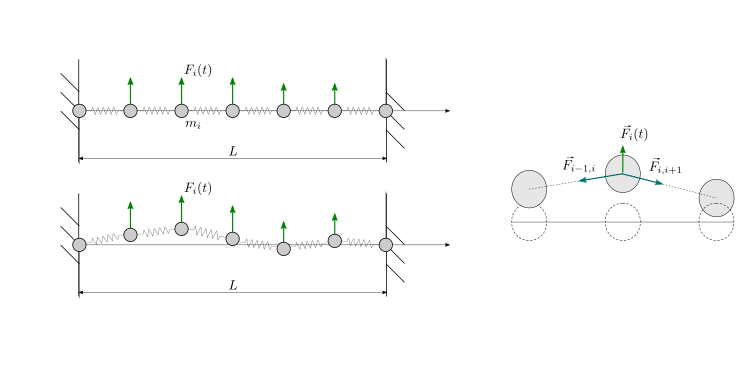
Fig. 21.3 Modello discreto di un filo teso.

21.1.2. Fluidi

21.1.2.1. Suono

La percezione umana dell’udito è legata alla trasduzione di perturbazioni di pressione di ampiezza limitata da parte del nostro sistema di misura che va dall’orecchio al nostro cervello, capace di percepire perturbazioni di frequenza compresa qualitativamente tra \(20 \, \text{Hz}\) e \(20.000 \, \text{Hz}\).

E” possibile ricavare l’equazione delle onde per il campo di pressione usando le equazioni di bilancio per sistemi aperti di massa e di quantità di moto, applicati a dei volumi elementari del dominio di interesse.

Si assume qui che il fluido nel quale si propaga la perturbazione acustica sia in quiete. Il calcolo viene inizialmente svolto in un ambito di spazio e variaili discrete, e solo alla fine vengono riconosciute le espressioni approssimate alle differenze delle derivate per tornare a un modello continuo. Si assume una dimensione uniforme dei domini elementari.

21.1.2.1.1. Dominio 1-dimensionale

Si considerano serie di elementi…e si scrive il bilancio di massa per gli elementi con indice intero, e il bilancio di quantità di moto per i volumi di indice frazionario «adiacenti»

\[\begin{split}\begin{aligned} \Delta x \, \dot{\rho}_i & = \overline{\rho} u_{i-\frac{1}{2}} - \overline{\rho} u_{i+\frac{1}{2}} \\ \Delta x \, \overline{\rho} \dot{u}_{i-\frac{1}{2}} & = P_{i-1} - P_{i} \\ \Delta x \, \overline{\rho} \dot{u}_{i+\frac{1}{2}} & = P_{i } - P_{i+1} \end{aligned}\end{split}\]

Derivando in tempo il bilancio della massa dell’elemento \(i\) e sostituendo in esso le due espressioni del bilancio della quantità di moto degli elementi \(i-\frac{1}{2}\) e \(i+\frac{1}{2}\) si ottiene

\[\Delta x \ddot{\rho}_i = \frac{1}{\Delta x} \left[ P_{i-1} - 2 P_i + P_{i+1} \right] \ ,\]

e ricordando la definizione di velocità del suono \(a\) todo (data dove? Forse è proprio questo il posto dove darla, assumendo una relazione lineare - tanto tutto o quasi è lineare nel piccolo - tra la perturbazione di pressione e la pertubazione di densità \(P_i = a^2 \rho_i\)), si può scrivere

\[\frac{1}{a^2} \ddot{P}_i - \dfrac{P_{i-1} - 2 P_i + P_{i+1}}{\Delta x^2} = 0 \ .\]

Avendo indicato il valore della pressione in \(x_k\) come \(P_k = P(x_k)\), si può riconoscere l’approssimazione della derivata seconda della pressione, e tornando al continuo e ricordando il significato di derivata parziale, ricavare l’equazione delle onde per la perturbazione di pressione in un mezzo in quiete[^medium-at-res]

\[\frac{1}{a^2} \partial_{tt} P - \partial_{xx} P = 0 \ .\]

Osservazione. Il metodo descritto qui rappresenta un’applicazione elementare del metodo dei volumi finiti, metodo utilizzato per la soluzione numerica di equazioni differentiali.

21.1.2.1.2. Dominio n-dimensionale

Si può ripetere il procedimento per un dominio 1-dimensionale in un dominio \(n\)-dimensionale, usando due suddivisioni «sfalsate» del dominio, una per calcolare il bilancio di massa, l’altra per calcolare il bilancio di quantità di moto. Ripendo il procedimento, si arriva a un’equazione che contiene l’approssimazione dell’operatore laplaciano della pressione,

\[\begin{split}\begin{aligned} \text{2-d:} & \quad \dfrac{P_{i-1,j-1}+P_{i-1,j+1}+P_{i+1,j+1}+P_{i+1,j-1}-4 P_{i,j}}{\Delta x^2} \sim \partial_{xx} P_i + \partial_{yy} P_i \\ \text{3-d:} & \quad \dfrac{P_{i-1,j-1,k-1}+\dots + P_{i+1,j+1,k+1}-8 P_{ijk}}{\Delta x^2} \sim \partial_{xx} P_i + \partial_{yy} P_i + \partial_{zz} P_i \\ \end{aligned}\end{split}\]

Per motivi di sintesi e per motivi di comprensione, l’approssimazione del laplaciano della pressione può essere scritta come sommatoria delle differenze della pressione nei domini \(\mathbf{j}\) vicini al dominio \(\mathbf{i}\), cioè appartenenti a quella che viene definita bolla di \(\mathbf{i}\), \(\mathbf{j} \in B(\mathbf{i})\),

\[\nabla^2 P_i \sim \dfrac{\sum_{\mathbf{j} \in B(\mathbf{i})}\left( P_{\mathbf{j}} - P_{\mathbf{i}} \right)}{\Delta x^2} \ .\]

Example 21.2 (Dominio \(2\)-dimensionale)

Example 21.3 (Dominio \(3\)-dimensionale)

21.1.2.2. Onde su superficie libera

21.1.3. Campo elettromagnetico