12.10. Problemi#
Questa pagina contiene esercizi di dinamica relativi a diversi argomenti: moto di un punto materiale, moto di sistemi di punti materiali, moto di corpi rigidi in due dimensioni, urti e collisioni, gravitazione, equilibrio e stabilità. Alcuni esercizi richiedono l’uso di principi di conservazione.
Argomenti: vedi alla fine file. Uncomment
moto di sistemi di punti
sistemi estesi con corpi rigidi in 2d
collisioni
gravitazione
equilibrio e stabilità
Una palla di massa \(m\) si trova inizialmente in quiete rispetto a un’osservatore inerziale, a una quota \(h\) sopra la superficie terrestre. La palla viene lasciata cadere dalla condizione di quiete. Viene chiesto di determinare:
la velocità di impatto con il terreno
il tempo impiegato per raggiungere il terreno.
Viene chiesto di svolgere i conti trascurando la resistenza dell’aria. Si chiede poi di:
confrontare i risultati ottenuti con i risultati per un corpo di massa \(M > m\)
confrontare i risultati ottenuti con i risultati che si otterrebbero nei pressi della superficie lunare.
Raggio Terra: \(R_E = 6380 \, km\) ; massa Terra: \(M_E = 5.98 \cdot 10^{24} \, kg\); Raggio Luna: \(R_M = 1740 \, km\) ; massa Luna: \(M_M = 7.34 \cdot 10^{22} \, kg\);

Soluzione.
Accelerazione nei pressi della superficie di un pianeta. L’accelerazione di gravità nei pressi della superficie di un pianeta è data dalla formula todo ref
Ricordando il valore della costante di gravitazione universale, \(G = 6.67 \cdot 10^{-11} \ \frac{N m^2}{kg^2}\), il campo di accelerazione di gravità nei pressi della superficie di Terra e Luna vale rispettivamente
Il rapporto tra le accelerazioni di gravità è \(\frac{g_E}{g_M} \sim 6.125\), mentre la radice di questo rapporto - che compare nell’ultimo punto di questo esercizio - è \(\sqrt{\frac{g_E}{g_M}} \sim 2.5\).
1. Velocità di impatto con il terreno. La velocità di impatto con il terreno può essere ricavata o dalla soluzione delle equazioni del moto, o dalla legge di conservazione dell’energia meccanica per sistemi conservativi: si considera qui il sistema «palla», sul quale agisce la forza di gravità - come manifestazione del campo di gravità del pianeta sui corpi con massa; se:
si trascura la resistenza dell’aria - azione non-conservativa, che verrà considerata nel problema successivo -
si considera il moto libero, prima dell’impatto a suolo - in generale le collisioni sono non-conservative, ad eccezione dell’unico caso particolare delle collisioni perfettamente elastiche
sul sistema non agiscono forze non-conservative; in assenza di azioni non-conservative, l’energia meccanica del sistema si conserva.
L’energia meccanica del sistema è la somma dell’energia cinetica e di quella potenziale: poiché solo la gravità agisce sul sistema, nell’energia potenziale compare solo il contributo gravitazionale - nella forma approssimata in prossimità della superficie di un pianeta,
Se il corpo è in caduta libera senza velocità orizzontale, il moto si svolge lungo la verticale. Il moto può quindi essere descritto con una coordinata sola: qui si sceglie un sistema di coordinate \(y\) con origine in corrispondenza del terreno e direzione positiva verso l’alto. L’energia meccanica del sistema può quindi essere scritta come
Nella condizione iniziale «0», il corpo è in quiete quindi la velocità è nulla. Nella condizione «1» poco prima dell’impatto, la quota è nulla rispetto al riferimento. Dall’uguaglianza \(E_0 = E_1\) segue
e quindi
2. Caloclo del tempo di volo. Per il calcolo del tempo di volo è necessario risolvere le equazioni del moto. Il bilancio della quantità di moto lungo \(y\),
diventa
con le condizioni iniziali \(y(0) = h\), \(\dot{y}(0) = 0\). Si semplifica la massa del sistema nell’equazione (per \(m \ne 0\)), e si integra due volte in tempo per risolvere l’equazione differenziale
Usando le condizioni iniziali, si trovano i valori delle costanti di integrazione \(v_0 = 0\), \(y_0 = h\). La legge del moto diventa quindi
Lo stato del sistema poco prima dell’urto si ottiene imponendo la condizione \(y(t_1) = 0\) e quindi si ottiene il tempo di volo (e si ri-ottiene il risultato della velocità di impatto già ottenuto con la conservazione dell’energia, con il segno negativo a indicare la direzione della velocità opposta al verso positivo dell’asse \(y\) utilizzato)
3. Risultati per un corpo di massa \(M > m\). Nelle ipotesi del problema di trascurare la resistenza aerodinamica del corpo, i risultati ottenuti non contengono la massa \(m\) del sistema, e quindi non dipendono da essa.
4. Risultati nei pressi della superficie lunare. I risultati nei pressi della superficie lunare si ottengono usando l’accelerazione \(g_M\) nelle formule. Confrontando i tempi e le velocità e usando i valori calcolati a inizio esercizio, si ottiene
un tempo di volo sulla Luna che è circa \(2.5\) volte quello sulla Terra, e una velocità di impatto circa \(\frac{1}{2.5}\) quella sulla Terra.
Viene chiesto di svolgere l’esercizio precedente, in un ambiente in cui non sia più trascurabile la resistenza aerodinamica del sistema. In particolare viene chiesto di risolvere il problema nel caso in cui la resistenza aerodinamica sia:
proporzionale alla velocità relativa del corpo rispetto al fluido, di intensità \(F = c v\), con \(c = \dots\)
proporzionale al quadrato della velocità relativa del corpo rispetto al fluido, di intensità \(F = \frac{1}{2} \rho S c_F v^2\), con…
Qui si considera il fluido in quiete rispetto all’ambiente: la velocità del corpo relativa al fluido è quindi uguale alla velocità rispetto all’ambiente.
Viene chiesto poi di determinare la velocità limite raggiungibile da un corpo in caduta libera, potendo considerare l’accelerazione di gravità e la densità dell’aria costanti lungo la caduta.
Soluzione.
1. Resistenza aerodinamica \(\propto v\). L’equazione del moto, con condioni iniziali \(y(0) = h\), \(\dot{y}(0) = 0\), è
o in termini di velocità
che può essere riscritta separando la forzante e mettendo in evidenza l’espressione classica delle equazioni differenziali ordinarie lineari a coefficienti costanti
La soluzione dell’equazione per la veloctià è la somma della soluzione generale dell’equazione omogenea e di una soluzione particolare,
e l’espressione della posizione si ottiene da una seconda integrazione
Le condizioni iniziali permettono di ricavare il valore delle costanti di integrazione \(A, B\)
La velocità di impatto con il terreno e il tempo di volo si ottengono dalla condizione \(y(t_1) = 0\) todo
La velocità limite è la velocità massima (in modulo) che viene raggiunta per \(t \rightarrow +\infty\), e quindi
\[v_{y,+\infty} = - \frac{m g}{c} \ .\]Si osservi come la velocità limite dipende dalla massa del corpo, e a parità di gravità e resistenza aerodinamica del corpo, un corpo con massa maggiore raggiunge una velocità limite maggiore (in modulo). …
Osservazione. Nel limite di resistenza aerodinamica che tende a zero, e per intervalli di tempo sufficientemente ridotti da avere \(\frac{ct}{m}\) «piccolo» (a sufficienza da rendere accettabile questa approssimazione) il termine \(e^{-\frac{ct}{m}}\) può essere approssimato come
e quindi
2. Resistenza aerodinamica \(\propto v^2\). Per studiare il moto del sistema con resistenza aerodinamica proprozionale al quadrato della velocità conviene usare un sistema di riferimento con origine nella posizione iniziale del sistema e una coordinata con il verso positivo verso il basso. Se inizialmente il corpo è in quiete o ha una velocità verso il basso, il moto non si inverte mai (e la velocità ha sempre lo stesso segno). L’equazione del moto,
con \(\dot{x} > 0\) può quindi essere riscritta rimuovendo il valore assoluto. Come fatto in precedenza, prima si scrive l’equazione in funzione della velocità, la si risolve, e successivamente si integra la velocità per trovare lo spazio. Usando la velocità \(\dot{x} = v\) come funzione dipendente, l’equazione del moto diventa
La velocità limite corrisponde alla condizione in cui la velocità non varia, e quindi la sua derivata è nulla \(\overline{v} = \sqrt{\frac{mg}{k}}\). Questa velocità può essere raggiunta da velocità inferiori ad essa (come ad esempio da un corpo che parte da fermo, accelerato dalla gravità), o da velocità superiori ad essa (come ad esempio un proiettile sparato a velocità superiori ad essa, rallentato dalla resistenza aerodinamica). Si può dimostrare todo che questa condizione di equilibrio è una condizione stabile: una volta nella condizione limite, un rallentamento del sistema comporterebbe una riduzione (in valore assoluto) della resistenza aerodinamica, e quindi una nuova accelerazione che comprterebbe un aumento della velocità del sistema (in assenza di variazioni di altre condizioni).
Questa equazione differenziale può essere risolta con il metodo di separazione delle variabili, riscrivendola nella forma
Scrivendo la frazione come somma di frazioni,
e riconoscendo l’itegrale del logaritmo (ed eliminando il modulo, considerando una velocità iniziale minore della velocità limite \(\sqrt{\frac{mg}{k}}\), e quindi sempre minore di essa), dall’integrazione si ricava
con la costante di integrazione nulla per la condizione iniziale \(v(0) = 0\).
e quindi
L’integrazione con le condizioni iniziali del problema fornisce la posizione in funzione del tempo
Riconoscendo la forma del differenziale di una funzione \(e^{-a t}\), \(d\left( e^{-a t} \right) = - a e^{-a t} dt\), e quindi di una funzione \(c + e^{-at}\) con \(c\) costante, \(d \left( c + e^{-at} \right) = - a e^{-a t} dt\), gli integrali della forma del secondo possono essere risolti come
Ricordando la condizione iniziale \(x(0) = 0\) quindi la posizione del sistema in funzone del tempo ha l’espressione
Osservazione. Per piccoli valori della resistenza aerodinamica e intervalli di tempo limitati, si ritrova la soluzione che trascura la resistenza aerodinamica. Infatti
può essere scritto nella form \(\ln (1+x)\) per «piccoli» \(x\) e approssimato con la sua serie di Taylor.
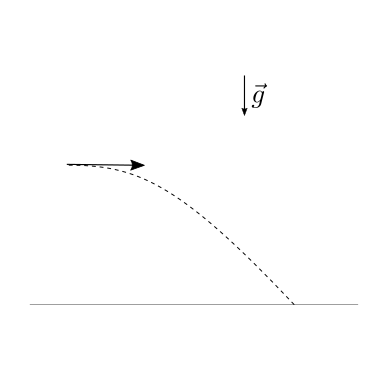
Un corpo di massa \(m\) viene lanciato con velocità iniziale orizzontale con valore assoluto \(|\vec{v}_0|\), da una quota \(h\) sopra la superficie terrestre. Trascurando la resistenza aerodinamica, viene chiesto di determinare:
gittata
tempo di volo
velocità del corpo all’impatto con il suolo
impulso e forza media quando il corpo raggiunge terra, sapendo che il corpo si arresta in un tempo \(\Delta t\) lungo una traiettoria rettilinea (l’ipotesi sulla traiettoria non è necessaria, come sarà chiaro nella soluzione dell’esercizio).
Come ulteriore esercizio, si ripetano i conti senza trascurare la resistenza aerodinamica.
Soluzione.
Gittata e tempo di volo possono essere ricavati dalla soluzione delle equazioni del moto con le opportune condizioni iniziali. Si sceglie di usare un sistema di coordinate cartesiane \(x\), \(y\) con origine nel punto iniziale, con l’asse \(x\) positivo verso destra e l’asse \(y\) positivo verso il basso. Usando questo sistema di coordinate, il vettore posizione del punto può essere scritto come
Il bilancio della quantitò di moto del sistema
con le condizioni iniziali \(\vec{r}_P(0) = \vec{0}\), \(\dot{\vec{r}}_P(0) = \vec{v}_0 = v_0 \hat{x}\) può essere scritto nelle sue coordinate cartesiane come
La posizione del corpo può quindi essere espressa in funzione del tempo,
e, con le condizioni iniziali del problema, posizione e velocità (derivata della posizione) del corpo in funzione del tempo \(t\) sono
1. - 2. Gittata e tempo di volo. La condizione di impatto prevede che il corpo percorra una distanza \(h\) in direzione \(y\) per raggiungere la superficie orizzonatale, e quindi può essere scritta come
Dalle due componenti cartesiane della posizione segue quindi
e quindi il tempo di volo \(t_1\) e la gittata \(d\) sono rispettivamente
3. Velocità del corpo all’impatto. Può essere calcolata usando le equazioni del moto già ricavate, o la conservazione dell’energia meccanica - in assenza di resistenza aerodinamica - come fattto in altri esercizi. Usando le equazioni già ricavate,
4. Impluso e forza media nell’impatto. L’impulso delle forze esterne agenti su un corpo equivale alla differenza del momento della quantità di moto todo aggiungere riferimento
e quindi
poiché la quantità di moto del corpo dopo essersi fermato è nulla, \(\vec{Q}_2 = \vec{0}\). L’impulso di una forza è il suo integrale nel tempo,
Gli istanti di tempo sono separati da \(\Delta t\), \(t_2 = t_1 + \Delta t\). La definizione di valore medio di una quantità in un intervallo permette di scrivere l’integrale come prodotto dell’intervallo e del valore medio, e quindi
e quindi
Viene chiesto di determinare:
la gittata massima di un corpo di massa \(m\) e velocità iniziale con valore assoluto \(|\vec{v}_0|\), trascurando la resistenza aerodinamica. Per questa condizione viene chiesto di determinare angolo iniziale rispetto all’orizzontale, tempo di volo e altezza massima raggiunta.
Viene poi chiesto di ripetere lo stesso esercizio:
non conoscendo la velocità iniziale, ma che il corpo viene inizialmente lanciato da un meccanismo in grado di applicare un impulso \(I\) noto ai corpi.
senza trascurare la resistenza aerodinamica

Soluzione.
1. Gittata massima. Usando un sistema di coordinate cartesiane (origine, assi,…)
con le condizioni iniziali \(x(0) = 0\), \(y(0) = 0\), \(v_x(0) = v_0 \cos \theta\), \(v_y(0) = v_0 \sin \theta\)
La condizione di impatto (insieme alla condizione di lancio) è \(y(t^*) = 0\),
ed è soddisfatta agli istanti di tempo \(t_0 = 0\) (lancio) e
Riconoscendo il seno di \(2 \theta\), \(\sin 2 \theta = 2 \sin \theta \cos \theta \) (todo link alle proprietà delle funzioni trigonometriche), la gittata diventa
Il massimo della gittata si trova per \(\sin 2 \theta^* = 1\), e quindi per \(\theta^* = \frac{\pi}{4} = 45^\circ\). Il tempo di volo è quindi
e la quota massima raggiunta (raggiunta per \(v_y(t_2) = y'(t_2) = 0\), \(t_2 = \frac{v_0}{g} \sin \theta^*\)) è
2. Noto l’impulso. La relazione tra l’impulso e la differenza di quantità di moto (tra la condizione di quiete, \(\vec{v}_{rest} = \vec{0}\) e il moemnto immediatamente successivo al lancio) è
Noto il legame tra \(\vec{I}\) e \(\vec{v}_0\), si possono usare i risultati del punto 1. dell’esercizio. Si osservi che dato l’impulso, la velocità \(\vec{v}_0\) è inversamente proporzionale alla massa \(m\) del sistema che viene accelerato: è infatti più difficile accelerare un corpo pesante rispetto a uno più leggero.
3. Considerando la resistenza aerodinamica.
Conoscendo la posizione del punto di lancio \(A\), e la posizione del bersaglio \(B\) viene chiesto di determinare:
le condizioni sulla velocità di lancio per colpire il bersaglio. Una volta determinate, viene chiesto di determinare anche il tempo di volo.
tra tutte le velocità ammissibili per colpire il bersaglio, viene chiesto di determinare quella con valore assoluto minimo, sotto al quale non è possibile raggiungere l’obiettivo.
Come ulteriore esercizio, si ripetano i conti senza trascurare la resistenza aerodinamica.

Soluzione.
Il bersaglio in \(\vec{r}_1 = x_1 \, \hat{x}_1 + y_1 \, \hat{y}_1\) viene colpito se la traiettoria passa per quel punto,
e quindi - moltiplicando per \(v_{x0}^2\) - si trova la relazione tra le coordinate della velocità
…todo… verificare se si può ottenere l’equazione di una conica…
Conoscendo la posizione del punto di lancio \(A\), e la posizione del bersaglio mobile \(B: \vec{r}_B(t) = x_B \hat{x} + (y_{B,0} + v_{y,B} t) \hat{y}\) viene chiesto di determinare:
le condizioni sulla velocità di lancio per colpire il bersaglio. Una volta determinate, viene chiesto di determinare anche il tempo di volo.
tra tutte le velocità ammissibili per colpire il bersaglio, viene chiesto di determinare quella con valore assoluto minimo, sotto al quale non è possibile raggiungere l’obiettivo.
Come ulteriore esercizio, si ripetano i conti senza trascurare la resistenza aerodinamica.

Soluzione.
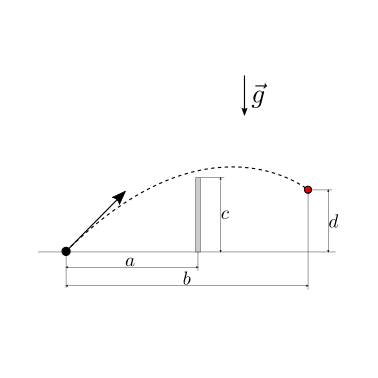
Un calciatore deve tirare una punizione in porta da una distanza \(b\). La barriera viene posta a una distanza \(a\) dal punto di tiro e i giocatori in barriera possono coprire fino a una quota \(h\) saltando. Volendo centrare la porta a una quota \(d\) (compresa tra \(0\): la palla tocca terra sulla linea di porta senza rimbalzare prima; e \(d_{max}\) la palla finisce all’incrocio), si chiede di determinare:
velocità iniziale imposta al pallone dal calcio
tempo di volo del pallone tra il calcio e la porta
in tutte le condizioni che permettono di prendere la porta senza colpire la barriera, e senza far rimbalzare il pallone prima della linea della porta. Per ogni valore \(d\), si calcoli poi la condizione che corrisponde al tempo minore.
Si trascuri ogni effetto, dovuto alla rotazione del pallone.
Si svolga l’esercizio prima trascurando e poi considerando la resistenza aerodinamica.
todo Si può ampliare un po” l’esercizio considerando i tempi di reazione del portiere e la velocità nel comprire le distanze? O formulare qualche metodo per stimare la probabilità di realizzazione di calci di punizione…
Soluzione.
La traiettoria è
Chiamando le coordinate \(x_1 = b\), \(y_1 = d\), il passaggio per il punto si ottiene dalla condizione
con la quale è possibile esprimere la componente \(v_{y0}\) in funzione della componente \(v_{x0}\) (che rimane così l’unico parametro libero del sistema) e degli altri parametri del sistema
La condizione che la palla superi la barriera (\(x_2 = a\), \(y_2 = c\)) può essere riscritta come
e quindi
In questa disequazione, il termine \(x_1 - x_2\) è positivo; il termine \(y_2 - \frac{x_2}{x_1} y_1\) può essere positivo o negativo: se negativo, la disequazione è sempre soddisfatta (è negativo nel caso in cui la traiettoria ottenibile con una velocità infinita, al limite, è possibile, cioè quando \(\frac{y_2}{x_2} < \frac{y_1}{x_1}\)), se positivo, si può scrivere
che implica che esiste un valore massimo per \(v_{x0}\), che quindi soddisfare la condizione
Il tempo di volo è
ed è quindi minimo quando \(v_{x0}\) è massimo, e quindi quando \(v_{x0} = \overline{v}_{x0}\). In questo caso, il rapporto tra la componente verticale e orizzontale della velocità iniziale è
Esempio numerico. Valutiamo due scelte di tiro per una punizione calciata dai \(x_1 = 20 \, m\) con barriera distante \(x_2 = 9.15 \, m\) che salta fino a \(y_2 = 2.5 \, m\). Si vuole valutare le scelte: A) tiro all’incrocio \(y_{1,A} = 2.2 \, m\); B) tiro che si abbassa dopo la barriera fino a \(y_{1,B} = 0.2 \, m\).
A. \(\overline{v}_{x0} = 18.05 \, m/s \), \(\overline{v}_{y0}/\overline{v}_{x0} = 0.411\), \(v_{y0} = 7.42 \, m/s \), \(|\vec{v}_{0}| = 19.51 \, m/s = 70.2 \, km/h\), \(\theta = 22.3^\circ\). \(t = 1.11 \, s\)
B. \(\overline{v}_{x0} = 14.21 \, m/s \), \(\overline{v}_{y0}/\overline{v}_{x0} = 0.495\), \(v_{y0} = 7.04 \, m/s \), \(|\vec{v}_{0}| = 15.86 \, m/s = 57.1 \, km/h\), \(\theta = 26.3^\circ\), \(t = 1.41 \, s\)
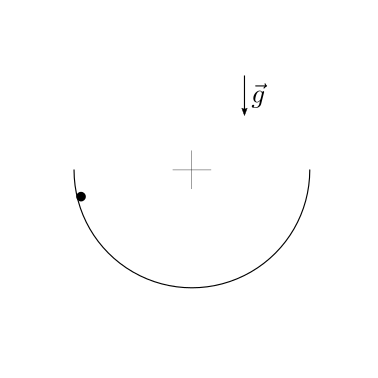
Un corpo puntiforme di massa \(m\) è vincolato a una guida semi-circolare con un vincolo bilatero ideale (no attrito, solo reazione normale). Il corpo parte in condizioni di quiete da una posizione identificata da un raggio che forma un angolo \(\theta_0\) con la verticale. Viene chiesto di:
rappresentare il diagramma delle forze agenti sul corpo;
scrivere l’espressione dell’energia meccanica del sistema, considerando il centro della semicriconferenza con punto di riferimento per definire l’energia potenziale gravitazionale nulla;
determinare la velocità massima del corpo nel suo moto
scrivere le equazioni del moto del sistema, usando se possibile: a) le equazioni cardinali della dinamica; b) la legge di conservazione dell’energia meccanica, c) altre leggi di conservazioni di quantità meccaniche costanti nella dinamica del sistema
determinare le reazioni vincolari della guida sul corpo puntiforme in funzione dell’angolo \(\theta\) e daella sua derivata \(\dot{\theta}\)
Soluzione.
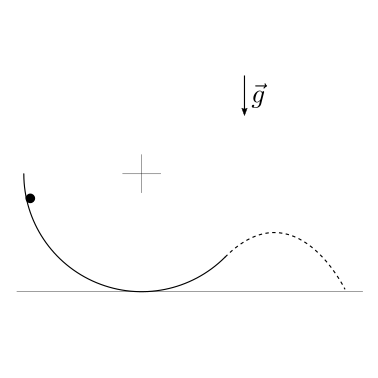
Un corpo puntiforme di massa \(m\) è vincolato a una guida ad arco di cerchio con un vincolo bilatero ideale. Viene lasciato cadere da un angolo \(\theta_0\) in condizioni di quiete. L’angolo «di uscita» della guida è \(\theta_1\). Se ragginge l’angolo di uscita, il corpo è libero di compiere la traiettoria caratteristica del moto libero nella prossimità della superficie terrestre. Viene chiesto di determinare:
la velocità massima del corpo lungo la guida,
le condizioni per venire lanciato fuori dalla guida
la traiettoria del moto libero, determinando in particolare la gittata, il tempo di volo e la velocità di impatto.
sapendo che all’impatto il corpo viene rallentato dal terreno lungo una traiettoria rettilinea con una decelerazione costante \(a\), si chiede di tereminare il tempo necessario all’arresto (a partire dall’impatto), l’impulso e la forza media.
Viene chiesto di discutere il problema considerando un attrito dinamico con coefficiente di attrito \(\mu_d\) tra la guida e il corpo, rappresentando il diagramma delle forze agenti sul corpo e determinando le equazioni del moto lungo la guida.
Soluzione.
Una guida è formata da un primo tratto di raggio \(R_1\), un secondo tratto di una circonferenza completa di raggio \(R_2 < R_1\) e un terzo tratto rettilineo orizzontale. Trascurando l’attrito nei primi due tratti, viene chiesto di determinare:
le condizioni necessarie per poter compiere il loop del secondo tratto, nel caso di vincolo bilatero
le condizioni necessarie per poter compiere il loop del secondo tratto, nel caso di vincolo monolatero
la distanza percorsa sul terzo tratto orizzontale, sul quale non è possibile trascurare l’attrito con la guida, rappresentabile con la formula dell’attrito dinamico con coefficiente \(\mu_d\).
Come esercizio aggiuntivo, viene chiesto di discutere il problema del moto del corpo con vincolo monolatero, nel caso in cui non sia in grado di compiere il loop.
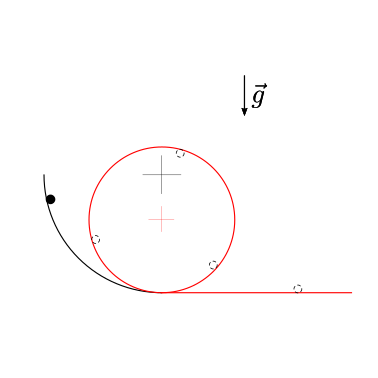
Soluzione.
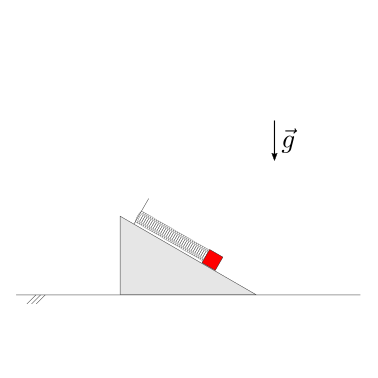
Conoscendo la configurazione iniziale della massa \(m\), viene chiesto di descrivere la dinamica del sistema nel caso di attrito nullo e nel caso di attrito non trascurabile. Viene chiesto di:
determinare le equazioni del moto
risolvere le equazioni del moto
determinare le reazioni vincolari scambiate tra massa e parete obliqua
determinare la forza scambiata tra molla e parete, in funzione del tempo

Soluzione.
Testo

Soluzione.
Testo

Soluzione.
Testo
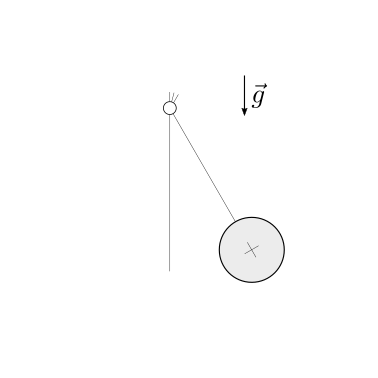
Soluzione.
Testo
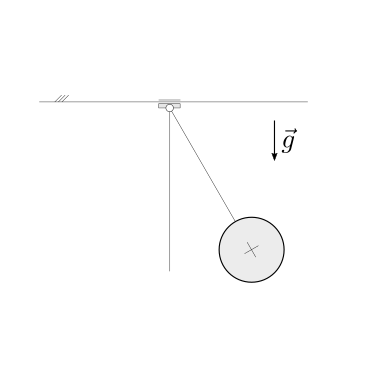
Soluzione.
Testo
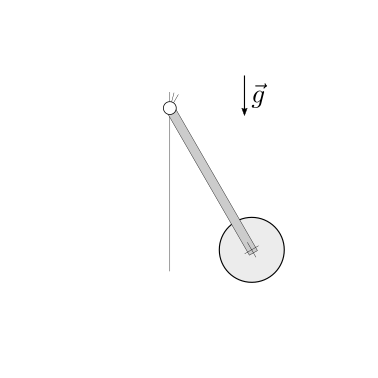
Soluzione.
Testo

Soluzione.
Testo

Soluzione.
I due solidi mostrati in figura sono collegati da una molla ideale lineare di costante elastica \(k\). Il sistema è inizialmente tenuto in quiete, con allungamento della molla \(x_0\). Nell’ipotesi sia possibile trascurare l’attrito tra i corpi, viene chiesto di determinare:
le espressioni dell’energia meccanica e della quantità di moto del sistema, e i loro valori
il modulo della velocità massima dei due corpi rispetto a un osservatore inerziale
le equazioni dinamiche del moto, e se possibile risolverle
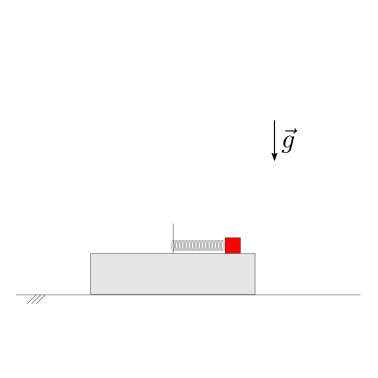
Soluzione.
Leggi di conservazione. In assenza di attrito tra il solido inferiore e la parete orizzontale, sul sistema formato dai due solidi collegati dalla molla non agiscono forze esterne in direzione orizzontale: è conservata quindi la componente orizzontale della quantità di moto del sistema. In assenza di attrito, sul sistema non agiscono azioni non conservative (gravità è conservativa, molla ideale è conservativa, e la reazione del vincolo non compie lavoro in assenza di attrito): è conservata quindi l”energia meccanica del sistema.
Scelta dei gradi di libertà. Sia \(x\) la posizione relativa della solido 2 rispetto al solido 1, coincidente con l’allungamento della molla; sia \(y\) la posizione del solido 1 rispetto all’osservatore inerziale.
L’energia meccanica del sistema è data dalla somma della sua energia cinetica e dalla sua energia potenziale, qui dovuta solo alla molla (i baricentri dei corpi non cambiano quota, quindi l’azione gravitazionale non compie lavoro). In un momento generico, quindi
\[E = K + V = \frac{1}{2} m_1 \dot{y}^2 + \frac{1}{2} m_2 \left( \dot{x} + \dot{y} \right)^2 + \frac{1}{2} k x^2 \ .\]e poiché il sistema è inizialmente in uno stato di quiete, l’energia meccanica vale \(E = E_{0} = \frac{1}{2} k x_0^2\).
La quantità di moto del sistema è data dalla somma delle quantità di moto delle sue parti. La componente orizzontale è quindi
\[Q_x = m_1 \dot{y} + m_2 \left( \dot{x} + \dot{y} \right) \ ,\]e poiché il sistema è inizialmente in uno stato di quiete, la componente orizzontale della quantità di moto vale \(Q_x = 0\). Da questa relazione si può quindi ricavare una relazione tra le derivate dei due gradi di libertà,
(12.11)#\[\dot{x} = - \frac{m_1 + m_2}{m_2} \dot{y}\]Usando la relazione (12.11), è possibile riscrivere l’espressione dell’energia meccanica del sistema in funzione solo di \(x\) e \(\dot{y}\)
\[E_0 = m_1 \dot{y}^2 + \frac{1}{2} k x^2 \ .\]Quindi la velocità massima dei due corpi si verifica quando l’allungamento della molla è nullo, \(x = 0\),
\[\begin{split}\begin{aligned} |v_{1,max}| & = |\dot{y}|_{max} && = \sqrt{\frac{E_0}{m_1}} \\ |v_{2,max}| & = |\dot{x}+\dot{y}|_{max} && = \frac{m_1}{m_2}\sqrt{\frac{E_0}{m_1}} \\ \end{aligned}\end{split}\]Le equazioni dinamiche del moto possono essere ottenute ad esempio:
dalle equazioni del moto, come il bilancio della quantità di moto della massa 2, e il bilancio della quantità di moto del sistema composto dalle due masse
\[\begin{split}\begin{cases} m_2 (\ddot{x} + \ddot{y}) + k x = 0 \\ m_1 \ddot{y} + m_2 (\ddot{x} + \ddot{y}) = 0 \end{cases}\end{split}\]oppure, derivando le espressioni dell’energia meccanica e della componente orizzontale della quantità di moto (integrali del moto)
Ad esempio, calcolando le derivate degli integrali del moto,
\[\begin{split}\begin{cases} 0 = \dot{y} m_1 \ddot{y} + m_2 (\dot{x} + \dot{y}) (\ddot{x} + \ddot{y}) + k x \dot{x} \\ 0 = m_1 \ddot{y} + m_2 ( \ddot{x} + \ddot{y} ) = 0 \end{cases}\end{split}\]e usando la relazione (12.11) per esprimere \(\dot{x}\) in funzione di \(\dot{y}\) e semplificare questo ultimo termine nella prima delle due equazioni,
\[\begin{split}\begin{aligned} 0 & = \dot{y} \left[ m_1 \ddot{y} + m_2 \left( - \frac{m_1+m_2}{m_2} + 1\right) \left( \ddot{x} + \ddot{y} \right) - \frac{m_1 + m_2}{m_2} k x \right] = \\ & = \dot{y} \left[ m_1 \ddot{y} - m_1 (\ddot{x} + \ddot{y}) - \frac{m_1 + m_2}{m_2} k x \right] \end{aligned}\end{split}\]e quindi
\[\begin{split}\begin{cases} 0 = m_1 \ddot{x} + \frac{m_1 + m_2}{m_2} k x \\ 0 = m_1 \ddot{y} + m_2 ( \ddot{x} + \ddot{y} ) = 0 \end{cases}\end{split}\]Osservazione. Queste equazioni sono equivalenti a quelle trovate in precedenza con le equazioni del moto, poiché
\[m_2 (\ddot{x} + \ddot{y}) = m_2 \ddot{x} \left( 1 - \frac{m_2}{m_1 + m_2} \right) = m_2 \frac{m_1}{m_1 + m_2} \ddot{x} \ .\]
Testo. …
Il disco rotola senza strisciamento sul prisma: questo moto è garantito dall’attrito tra i due corpi. Osservazione. La forza scambiata tra i due corpi compie lavoro? No, poiché le forze scambiate tra i due corpi sono uguali e contrari e sono applicate in punti che hanno la stessa velocità per la condizione di puro rotolamento, vedi Esempi di forze - Azioni di contatto - Puro rotolamento.
Chiedere di studiare due condizioni:
assenza di attrito tra il prisma e la parete orizzontale: in assenza di azioni non-conservative, si può applicare il teorema di conservazione dell’energia meccanica
con attrito tra il prisma e la parete orizzontale: è necessario usare equaizoni dinamiche…
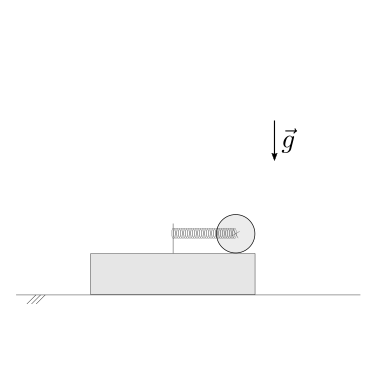
Soluzione.
Nelle condizioni di contatto tra prisma e superficie orizzontale, e di puro rotolamento tra disco e prisma, il sistema ha due gradi di libertà.
Cinematica. todo …descrizione della cinematica e scelta dei gradi di libertà…
Senza attrito. Per determinare le 2 equazioni del moto per i 2 gradi di libertà si possono usare 2 leggi di conservazione:
conservazione dell’energia meccanica, valido in assenza di azioni non-conservative
conservazione della componente orizzontale della quantità di moto del sistema completo, sul quale non agiscono azioni esterne nette con componente orizzontale diversa da zero.
Quantità dinamiche. Energia meccanica del sistema \(E^{mec} = K + V\),
Integrali del moto - quantità costanti.
confronto tra lo stato del sistema in due istanti temporali diversi…
Equazioni del moto. Poiché l’energia meccanica e la quantità orizzontale della quantità del sistema completo sono costanti del moto, si possono ricavare le equazioni del moto valutando la derivata nel tempo dell’espressione dei due integrali del moto,
La prima equazione può essere riscritta come
Con attrito. …
Testo
Soluzione.
Quantità dinamiche.
Integrali del moto.
Equazione del moto.
Riconoscendo nella seconda equazione, il fattore di \(\dot{x}\) uguale alla prima equazione e quindi nullo, le equazioni del sistema possono essere riscritte come equazioni dinamiche del secondo ordine
Testo

Soluzione.
Testo
Soluzione.
Testo
Soluzione.
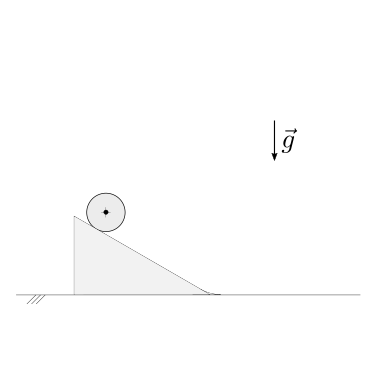
A un disco di massa \(M\) e raggio \(R\) e distribuzione di massa uniforme è connessa una massa concentrata \(m\) che può essere rappresentata da una massa puntiforme, posizionata a distanza \(R\) dal centro del disco. Il sistema inizialmente in quiete viene messo in moto da una coppia costante \(C\) fino a raggiungere la velocità angolare di regime \(\Omega\). Viene chiesto di determinare:
il momento di inerzia del sistema rispetto al centro di rotazione
il tempo necessario per raggiungere la velocità angolare \(\Omega\)
le reazioni vincolari in corrispondenza della cerniera
todo Commentare i risultati di questo esercizio con la resistenza a fatica dei materiali
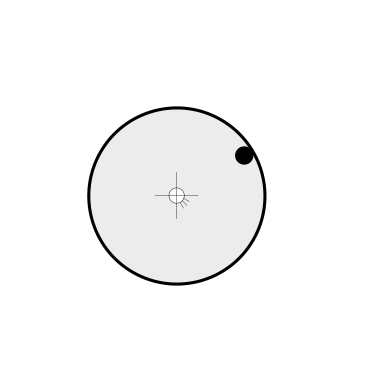
Soluzione.
Il momento di inerzia del sistema rispetto al centro di rotazione è uguale alla somma dei momenti di inerzia del disco e della massa concentrata, todo perché? Il momento angolare è una quantità additiva, ma il momento di inerzia? todo fare riferimento ai valori dei momenti di inerzia di disco e massa
\[I = I^{disk} + I^{mass} = \frac{1}{2} M R^2 + m R^2 \ .\]L’equazione di moto che governa la dinamica dell’angolo di rotazione del sistema \(\theta(t)\) può essere ricavata dall’equazione di bilancio del momento della quantità di moto, usando come polo \(A\) il centro del cerchio (polo fisso, \(\dot{\vec{x}}_A = \vec{0}\))
\[\frac{d L_A}{d t} = M^{ext}_A \ .\]Il momento della quantità di moto è la somma dei momenti della quantità di moto dei due sistemi. La sua componente perpendicolare al piano di rotazione vale
\[L_{A,z} = L_{A,z}^{disk} + L_{A,z}^{mass} = I^{disk} \dot{\theta} + m R^2 \dot{\theta} = I \dot{\theta} \ .\]L’equazione del moto quindi diventa
\[I \ddot{\theta} = C \ ,\]dove la derivata del momento angolare uguaglia la coppia esterna agente sul sistema. Se il sistema parte da una condizione di quiete e la coppia applicata è costante, è possibile integrare l’equazione del moto e trovare
\[\begin{split}\begin{aligned} \dot{\theta}(t) & = \frac{C}{I} \, t \\ \theta (t) & = \frac{1}{2} \frac{C}{I} \, t^2 \\ \end{aligned}\end{split}\]fino al raggiungimento della velocità di regime \(\Omega = \dot{\theta}(t^*) = \dfrac{C t^*}{I}\), nell’intervallo di tempo
\[t^* = \frac{I \Omega}{C} \ .\]Una cerniera cilindrica permette la rotazione del corpo attorno al proprio asse, mentre vincola completamente la traslazione del punto in cui viene connessa, con una forza come reazione vincolare. In un moto piano, la cerniera impedisce la traslazione in due direzioni e la reazione vincolare è una forza che viene determinata dalle sue due componenti nel piano.
Una volta noto il moto del sistema, \(\theta(t)\), le reazioni vincolari possono essere determinate ad esempio dall’equazione di bilancio della quantità di moto del sistema,
\[\dot{\vec{Q}} = \vec{R} \ .\]La quantità di moto del sistema è uguale alla somma delle quantità di moto delle sue parti. Il centro di massa del disco non trasla, e quindi la quantità di moto del disco è nulla. Usando un sistema di coordinate polari, si può scrivere la quantità di moto del sistema come
\[\vec{Q} = m \vec{v}_B = m R \dot{\theta} \hat{\theta} \ ,\]e la sua derivata,
\[\dot{\vec{Q}} = m R \ddot{\theta} \hat{\theta} - m R \dot{\theta}^2 \hat{r} \ .\]Dal bilancio della quantità di moto del sistema, si ottengono le azioni imposte dal vincolo sul sistema (quelle che agiscono sul vincolo sono uguali e contrarie, per il principio di azione/reazione),
\[\vec{R} = R_r \hat{r} + R_{\theta} \hat{\theta} = \dot{\vec{Q}} = m R \ddot{\theta} \, \hat{\theta} - m R \dot{\theta}^2 \, \hat{r} \ .\]
Testo
Soluzione.
Testo
Soluzione.
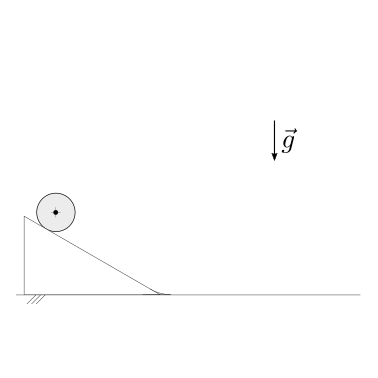
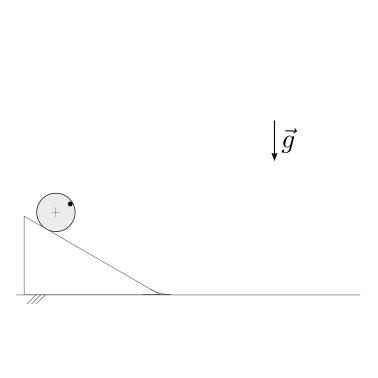
Un sistema puntiforme è libero di scivolare su una superficie semi-circolare con attrito trascurabile. Conoscendo la condizione iniziale, \(\theta(0) = \theta_0\), \(\dot{\theta}(0) = \Omega\), viene chiesto di determinare:
la condizione di distacco dalla superficie
la distanza di orizzontale del punto di atterraggio del corpo dopo il volo libero, rispetto alla superficie semicircolare.

Soluzione.
Il vincolo con la superficie è un vincolo ideale monolatero, che agisce solo fino a quando la componente radiale della reazione vincolare è positiva. Fino a quando il vincolo ideale monolatero è attivo - cioè fino a quando la massa scivola sulla superficie - il sistema ha un grado di libertà, qui scelto come l’angolo \(\theta\). Il distacco del corpo dalla superficie vine determinata dalla condizione \(R_r(\theta^*) = 0\). Successivamente al distacco, il sistema ha due gradi di libertà mentre compie un moto libero in un campo gravitazionale.
L’equazione di bilancio del momento della quantità di moto rispetto al centro della circonferenza permette di determinare un’equazione pura del moto del sistema
\[\frac{d L_{A,z}}{d t} = M_{A,z}^{ext} \ ,\]e quindi
\[m R^2 \ddot{\theta} = m g R \sin \theta\]con le condizioni iniziali definite dal problema. Oppure, la conservazione dell’energia meccanica
(12.12)#\[E = m g R \cos \theta + \frac{1}{2} m R^2 \dot{\theta}^2\]in assenza di azioni non conservative, permette di ricavare immediatamente una relazione tra \(\theta\) e \(\dot{\theta}\). L’equazione di bilancio della quantità di moto permette invece di determinare le reazioni vincolari,
\[\dot{\vec{Q}} = \vec{R}^e \ ,\]\[\begin{split}\begin{aligned} R_r \hat{r} + \underbrace{R_{\theta}}_{= 0 \text{ no friction}} \hat{\theta} + m \vec{g} & = \dfrac{d}{dt} \left( m R \dot{\theta} \hat{\theta} \right) = \\ & = m R \left( \ddot{\theta} \hat{\theta} - \dot{\theta}^2 \hat{r} \right) \end{aligned}\end{split}\]e quindi le due componenti radiale e tangenziale diventano
\[\begin{split}\begin{cases} r: \ R_r = m g \cos \theta - m R \dot{\theta}^2 \\ \theta: \ m g \sin \theta = m R \ddot{\theta}^2 \\ \end{cases}\end{split}\]La componente tangenziale è equivalente all’equazione pura del moto; la componente radiale fornisce l’espressione della reazione vincolare in funzione di \(\theta\) e \(\dot{\theta}\). Usando la relazione (12.12) per esprimere \(\dot{\theta}\) in funzione di \(\theta\), si può scrivere la reazione normale in funzione del solo \(\theta\)
\[\begin{split}\begin{aligned} R_r & = m g \cos \theta - m R \dot{\theta}^2 = \\ & = m g \cos \theta - \frac{2}{R} \left( E - m g R \cos \theta \right) = \\ & = 3 m g \cos \theta - \frac{2 E}{R} \ . \end{aligned}\end{split}\]La condizione \(R_r \ge 0\) equivale quindi alla condizione
\[\cos \theta \ge \frac{2}{3} \frac{E}{m g R}\]Nel caso in cui il sistema è inizialmente in quiete in corrispondenza del punto più alto della superficie e in quiete (o quel minimo di velocità per allontanarsi dalla posizione di equilibrio instabile), l’energia meccanica del sistema è \(E = m g R\) e l’angolo limite \(\theta^*\) ha coseno e seno
\[\begin{split}\begin{aligned} \cos \theta^* & = \frac{2}{3} \frac{E}{mgR} = \frac{2}{3} \\ \sin \theta^* & = \sqrt{1 - \cos^2 \theta^* } = \frac{\sqrt{5}}{3} \\ \end{aligned}\end{split}\]e la sua derivata vale
\[\begin{split}\begin{aligned} \dot{\theta}^* & = \sqrt{ \frac{2}{m R^2} \left( E - m g R \cos \theta^* \right) } = \\ & = \sqrt{ \frac{2}{m R^2} \left( m g R - m g R \frac{2}{3} \right) } = \sqrt{ \frac{2}{3} \frac{g}{R} } \ . \end{aligned}\end{split}\]Il moto libero è determinato dalle equazioni del moto
\[\begin{split}\begin{cases} m \ddot{x} = 0 \\ m \ddot{y} = -m g \\ \end{cases}\end{split}\]con le condizioni iniziali
\[\begin{split} \begin{cases} x(t_0) = R \sin \theta^* \\ y(t_0) = R \cos \theta^* \end{cases} \quad , \quad \begin{cases} v_x(t_0) = R \dot{\theta}^* \sin \theta^* \\ v_y(t_0) = - R \dot{\theta}^* \cos \theta^* \end{cases} \end{split}\]
Testo

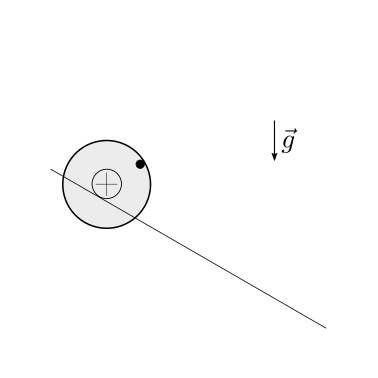
Soluzione.
Cinematica. Fino a quando il vincolo di contatto e puro rotolamento è soddisfatto, il sistema ha un solo grado di libertà effettivo. Si sceglie qui l’angolo \(\theta\) formato dalla direzione che congiunge i centri del disco e della semicriconferenca. La posizione e velocità del centro \(C\) del disco possono essere scritte usando un sistema di coordinate polari
Si calcola la velocità angolare del disco, \(\vec{\omega} = \omega \hat{z}\), usando la legge dell’atto di moto rigido confrontando il centre \(C\) con il punto di contatto \(Q\) (diverso a ogni istante di tempo) con la superficie semi-circolare,
Quando il vincolo di puro rotolamento è soddisfatto, la velocità del punto materiale del disco nel punto \(Q\) è nulla, poiché è uguale alla velocità del punto della calotta sferica a contatto - che è nullo poiché la calotta è fissa,
e quindi la velocità angolare in funzione della coordinata libera \(\theta\) è \(\omega = \frac{R + r}{r} \dot\theta\).
Equazioni della dinamica. Le equazioni della dinamica per il disco sono
avendo scelto il centro di massa \(C\) del disco per l’equazione del momento della quantità di moto. La quantità di moto e il momento della quantità di moto sono
e la derivata nel tempo è
Proiettando l’equazione della quantità di moto in direzione radiale e tangenziale, le componenti delle equazioni del moto sono
Sommando l’equazione della quantità di moto in direzione tangenziale moltiplicata per \(r\) e l’equazione del momento della quantità di moto, si ottiene un”equazione pura del moto nella quale non compaiono reazioni vincolari,
Questa equazione può essere manipolata per ottenere un’equazione di conservazione dell’energia meccanica, poiché sul disco non agiscono azioni non conservative: portando tutti i termini da una parte dell’uguale, moltiplicando per \(\frac{R+r}{r}\dot{\theta}\), e riconoscendo che
si può scrivere la legge di conservazione dell’energia meccanica
e quindi il valore dell’energia è costante,
Nel caso in cui il sistema si trovi nella condizione iniziale di quiete, \(\dot{\theta}_0 = 0\) e a contatto con il punto più alto della circonferenza, \(\theta_0 = 0\), \(\cos \theta_0 = 1\),
E” quindi possibile ricavare \(\dot{\theta}^2\) in funzione di \(\theta\),
e poi sostituire il valore nella componente radiale dell’equazione della quantità di moto per ricavare l’espressione della componente in direzione radiale della reazione vincolare
Nel caso di disco uniforme, il momento di inerzia è \(I = \frac{1}{2} m r^2\),
Nella condizione limite in cui il disco si stacca dal corpo, la componente radiale della reazione vincolare si annulla. Questo avviene in corrispondenza dell’angolo \(\theta^*\), il cui coseno vale
Conservazione dell’energia meccanica. In assenza di azioni non-conservative, si può risolvere l’esercizio usando l’equazione di conservazione dell’energia meccanica.
…
Testo

Soluzione.
Se avviene puro rotolamento del cerchio esterno sul terreno, e del disco sulla superficie interna del cerchio, il sistema ha due gradi di libertà, che descrivono due moti indipendenti: (1) il moto del cerchio esterno rispetto al terreno, (2) il moto del disco sulla superficie interna del cerchio.
Solution using Lagrangian mechanics
Lagrangian function. \(L = K + U\)
Kinetic energy.
\[ K = \dfrac{1}{2} m_A |\vec{v}_A|^2 + \dfrac{1}{2} I_A \omega_A^2 + \dfrac{1}{2} m_B |\vec{v}_B|^2 + \dfrac{1}{2} I_B \omega_B^2 \ .\]Potential function \(U = - V\).
\[U = - m g y_B\]
Kinematics.
Position and velocity of the center of the circle
\[\begin{split}\begin{aligned} A - O & = \hat{x} \, R \theta_A \\ \vec{v}_A & = \hat{x} \, R \dot\theta_A \\ \end{aligned}\end{split}\]Position and velocity of the center of the disc
\[\begin{split}\begin{aligned} B - A & = - \hat{x} \, (R-r) \sin \theta_B + \hat{y} \, (R - (R-r) \cos \theta_B) \\ \vec{v}_{B} - \vec{v}_A & = - \hat{x} \, (R-r) \dot{\theta}_B \cos \theta_B + \hat{y} \, (R-r) \dot\theta_B \sin \theta_B & \qquad \text{(a)} \\ \end{aligned}\end{split}\]\[\vec{v}_B = \hat{x} \left[ R \dot\theta_A - (R-r) \dot{\theta}_B \cos \theta_B \right] + \hat{y} \left[ (R-r) \dot\theta_B \sin \theta_B \right]\]\[| \vec{v}_B |^2 = R^2 \dot\theta_A^2 - 2 R (R-r)\dot\theta_A \dot\theta_B \cos \theta_B + (R-r)^2 \dot\theta_B^2 \ .\]Angular velocity of the circle, \(\vec{\omega}_A = - \dot\theta_A \hat{z}\)
Angular velocity of the disc, using pure rolling between the disc and the circle, and the kinematics of the circle to find the velocity of the contact point as a function of the state of the circle only,
\[\begin{aligned} \vec{v}_B - \vec{v}_Q = \vec{\omega}_{B} \times (B - Q) \ , & \qquad \text{(b)} \end{aligned}\]with
\[\begin{split}\begin{aligned} \vec{v}_Q & = \vec{v}_A + \vec{\omega}_A \times (Q - A) = \\ & = \vec{v}_A - \hat{z} \dot{\theta}_A \times \left( - \hat{x} R \sin \theta_B - \hat{y} R \cos \theta_B \right) = \\ & = \vec{v}_A - \hat{x} \, R \dot\theta_A \cos \theta_B + \hat{y} \, R \dot\theta_A \sin \theta_B \end{aligned}\end{split}\]And thus, comparing the two expressions of \(\vec{v}_B - \vec{v}_A\),
\[\begin{split}\begin{aligned} \text{(a)} & = - \hat{x} \, (R-r)\dot{\theta}_B \cos \theta_B + \hat{y} \, (R-r) \dot{\theta}_B \sin \theta_B = \\ \text{(b)} & = - \hat{x} R \dot\theta_A \cos \theta_B + \hat{y} R \dot \theta_A \sin \theta_B + \omega_B \hat{z} \times \left[ \hat{x} r \sin \theta_B + \hat{y} r \cos \theta_B \right] = \\ & = \hat{x} \left[ - R \dot\theta_A - r \omega_B \right] \cos \theta_B + \hat{y} \left[R \dot\theta_A + r \omega_B \right] \sin \theta_B \end{aligned}\end{split}\]it follows that
\[\begin{split}\begin{aligned} & (R-r )\dot\theta_B = R \dot\theta_A + r \omega_B \\ & \qquad \rightarrow \qquad \omega_B = -\dfrac{R}{r} \dot\theta_A + \frac{R-r}{r} \dot\theta_B \end{aligned}\end{split}\]
Lagrangian function.
with \(\vec{v}_B(\theta_A, \theta_B, \dot\theta_A, \dot\theta_B)\), and \(\omega_B(\theta_A, \theta_B, \dot\theta_A, \dot\theta_B)\).
Pure equations of motion from Largange equations of type II.
gives the conservation of generalized momentum w.r.t. \(\theta_A\). todo Physical meaning? What’s that conserved quantity? It could be something like the angular momentum of the system w.r.t. a pole w.r.t. the net moments of the external actions is zero
2\(^{nd}\) order dynamical equations of motion.
Equilibrium. Equilibriu is attained as the condition \(\sin \theta_B = 0\). It’s possible to prove (…prove it!) that \(\theta_B = 0\) is a stable equilibrium, while \(\theta_B = \pi\) would be unstable (if it constraints allows to reach it. With monolateral contacts, the normal reactions between bodies should be so that one body pushes the other, otherwise contact is lost. Unstable equilibrium is not possible to be reached with monolateral contacts, as the disk would fall under its weight. Discuss limit conditions? It could be another exercise…one more, one less…).
The value of angle \(\theta_A\) is irrelevant for the position of equilibrium, and for the problem in general, because of the symmetry of the system under investigation and the actions acting on it, not depending on \(\theta_A\). This condition is reflected in the result \(\dfrac{\partial L}{\partial \theta_A}\)
Linearized equations of motion around the equilibrium \(\ \theta_A = 0, \ \theta_B = 0\).
Lagrangian method provides a linearized system of the mechanical system of the form
with symmetri mass and stiffness matrices \(\mathbf{M} = \mathbf{M}^T\), \(\mathbf{K} = \mathbf{K}^T\), and semi-definite positive if the system is linearized around a (marginally)stable equilibrium, \(\mathbf{M} > 0\), \(\mathbf{K} \ge 0\).
Testo