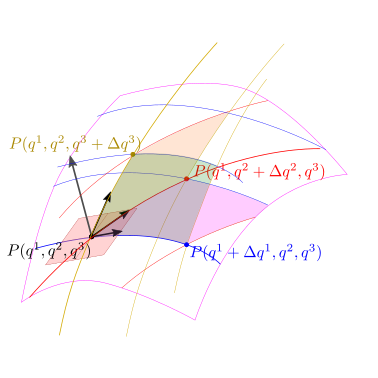28.1. Cenni di geometria differenziale

28.1.1. Parametrizzazione dello spazio

Uno spazio può essere descritto tramite l’uso di un sistema di coordinate, composto da una \(n\)-upla di coordinate indipendenti \(\left( q^i \right)_{i = 1:n}\).

Definition 28.1 (Parametrizzazione regolare)

Una parametrizzazione di una regione dello spazio spazio è regolare se è una funzione biunivoca,

\[P\left(q^i \right)\]

tra i punti \(P\) dello spazio e i valori delle coordinate \(\left( q^i \right)\). In altre parole, a ogni \(n\)-upla \(\left( q^i \right)_{i=1:n}\) corrisponde uno e un punto \(P\) e viceversa.

todo

• Conseguenze sulle funzioni delle coordiante dei punti in funzione delle coordiante: derivata non si annulla nel dominio…

• Può essere necessario/utile definire più parametrizzazioni che coprono diverse zone del dominio…

Example 28.1 (Spazio \(E^2\): coordinate cartesiane)

Dopo aver scelto il punto \(O\) come origine, è possibile utilizzare un sistema di coordinate cartesiane \((q^1, q^2) = (x,y)\) e rappresentare un generico punto \(P\) dello spazio come

\[\vec{r} = P - O = x \, \hat{x} + y \, \hat{y} \ .\]

Example 28.2 (Spazio \(E^2\): coordinate polari)

Utilizzando un sistema di coordinate polari con la stessa origine \(O\) di un sistema di coordinate cartesiane, e l’asse di riferimento per l’angolo \(\theta\) coincidente con l’asse \(x\) del sistema di coordinate cartesiane, è possibile rappresentare le coordinate cartesiane in funzione delle coordinate polari \((q^1, q^2) = (r, \theta)\)

\[\begin{split}\begin{cases} x = r \, \cos \theta \\ y = r \, \sin \theta \\ \end{cases}\end{split}\]

e un punto generico nello spazio - con una rappresentazione «mista» che usa le coordinate polari e i vettori \(\hat{x}\), \(\hat{y}\) ddella base cartesiana1 - come

\[\vec{r} = r \, \cos \theta \, \hat{x} + r \, \sin \theta \, \hat{y} \ .\]

Example 28.3 (Spazio \(E^3\): coordinate cartesiane)

Dopo aver scelto il punto \(O\) come origine, è possibile utilizzare un sistema di coordinate cartesiane \((q^1, q^2, q^3) = (x,y,z)\) e rappresentare un generico punto \(P\) dello spazio come

\[\vec{r} = P - O = x \, \hat{x} + y \, \hat{y} + z \, \hat{z} \ .\]

Example 28.4 (Spazio \(E^3\): coordinate cilindriche)

Utilizzando un sistema di coordinate polari con la stessa origine \(O\) di un sistema di coordinate cartesiane, gli assi \(z\) coincidenti, e l’asse di riferimento per l’angolo \(\theta\) coincidente con l’asse \(x\) del sistema di coordinate cartesiane, è possibile rappresentare le coordinate cartesiane in funzione delle coordinate polari \((q^1, q^2, q^3) = (r, \theta, z)\)

\[\begin{split}\begin{cases} x = r \, \cos \theta \\ y = r \, \sin \theta \\ z = z \end{cases}\end{split}\]

e un punto generico nello spazio - con una rappresentazione «mista» che usa le coordinate polari e i vettori \(\hat{x}\), \(\hat{y}\), \(\hat{z}\) della base cartesiana1 - come

\[\vec{r} = r \, \cos \theta \, \hat{x} + r \, \sin \theta \, \hat{y} + z \, \hat{z} \ .\]

Example 28.5 (Spazio \(E^3\): coordinate sferiche)

Utilizzando un sistema di coordinate polari con la stessa origine \(O\) di un sistema di coordinate cartesiane, gli assi \(z\) coincidenti, e l’asse di riferimento per l’angolo \(\theta\) coincidente con l’asse \(x\) del sistema di coordinate cartesiane, è possibile rappresentare le coordinate cartesiane in funzione delle coordinate polari \((q^1, q^2, q^3) = (R, \phi, \theta)\)

\[\begin{split}\begin{cases} x = R \, \sin \phi \, \sin \theta \\ y = R \, \sin \phi \, \cos \theta \\ z = R \, \cos \phi \end{cases}\end{split}\]

e un punto generico nello spazio - con una rappresentazione «mista» che usa le coordinate polari e i vettori \(\hat{x}\), \(\hat{y}\), \(\hat{z}\) della base cartesiana1 - come

\[\vec{r} = R \, \sin \phi \, \cos \theta \, \hat{x} + R \, \sin \phi \, \sin \theta \, \hat{y} + R \, \cos \phi \hat{z} \ .\]

28.1.1.1. Base naturale

La paramterizzazione dello spazio permette di associare a ogni punto dello spazio una \(n\)-upla di coordiante. Usando una rappresentazione mista - scegliendo dei vettori di una base cartesiana con origine in \(O\), e coordiante generiche \(q^i\) - si può quindi rappresentare i punti dello spazio utilizzando le coordinate \(q^i\) desiderate e i vettori della base cartesiana,

\[\vec{r} = P - O = x^k \left(q^i\right) \hat{x}_k \ ,\]

o più esplicitamente per spazi 2-dimensionali

\[\vec{r} = P - O = x \left(q^1, q^2\right) \hat{x} + y\left(q^1, q^2\right) \hat{y} \ ,\]

e per spazi 3-dimensionali

\[\vec{r} = P - O = x \left(q^1, q^2, q^3\right) \hat{x} + y\left(q^1, q^2, q^3 \right) \hat{y} + z\left( q^1, q^2, q^3 \right) \hat{z} \ .\]

Definition 28.2 (Base naturale)

In ogni punto dello spazio, è possibile definire i vettori della base naturale indotta da una particolare scelta del sistema di coordinate \(\left( q^i \right)_{i:n}\) come le derivata parziali del punto \(P\) rispetto alle coordinate \(q^i\). I vettori della base naturale \(\left\{\vec{b}_i \right\}_{i=1:n}\) indotta dalle coordinate \(\left( q^i \right)_{i=1:n}\) sono quindi i vettori

\[\vec{b}_i = \frac{\partial \vec{r}}{\partial q^i} \ .\]

In generale, come sarà chiaro dagli esempi, i vettori di una base naturale:

• dipendono dal punto nello spazio nel quale vengono calcolati - o in altre parole sono funzioni delle coordinate \(q^i\)

• non formano una base orto-normale

• non hanno lunghezza unitaria

• non sono omogenei nelle dimensioni, né adimensionali.

Definition 28.3 (Base fisica)

Nel caso in cui la base naturale sia ortogonale, è possibile definire una base fisica - orto-normale con vettori unitari e adimensionali - tramite un semplice processo di normalizzazione dei vettori della base,

\[\hat{b}_i := \frac{\vec{b}_i}{|\vec{b}_i|} \ .\]

La definizione di una base fisica, quando possibile, può rendere la rappresentazione di un vettore o di un campo vettoriale più «ordinata», avendo le componenti del vettore le stesse dimensioni fisiche della grandezza che viene rappresentata, poiché i vettori della base fisica sono adimensionali e di lunghezza unitaria - e quindi contenenti unicamente l’informazione vettoriale sulla direzione.

Example 28.6 (Spazio \(E^2\): coordinate cartesiane)

I vettori della base naturale sono

\[\begin{split}\begin{cases} \vec{b}_1 = \frac{\partial \vec{r}}{\partial x} = \frac{\partial }{\partial x} \left( x \hat{x} + y \hat{y} \right) = \hat{x} \\ \vec{b}_2 = \frac{\partial \vec{r}}{\partial y} = \frac{\partial }{\partial y} \left( x \hat{x} + y \hat{y} \right) = \hat{y} \\ \end{cases}\end{split}\]

Ricordando le proprietà dei vettori di una base cartesiana todo link, è immediato verificare che la base naturale di un sistema di coordinate cartesiane è anche la sua base fisica (adimensionale non-dimensionale).

Example 28.7 (Spazio \(E^2\): coordinate polari)

I vettori della base naturale sono

\[\begin{split}\begin{cases} \vec{b}_1 = \frac{\partial \vec{r}}{\partial r } = \frac{\partial }{\partial r } \left( r \cos \theta \hat{x} + r \sin \theta \hat{y} \right) = \cos \theta \hat{x} + \sin \theta \hat{y} \\ \vec{b}_2 = \frac{\partial \vec{r}}{\partial \theta} = \frac{\partial }{\partial \theta} \left( r \cos \theta \hat{x} + r \sin \theta \hat{y} \right) = -r\sin \theta \hat{x} + r \cos \theta\hat{y} \\ \end{cases}\end{split}\]

E” semplice dimostrare che i due vettori sono ortogonali, ma il vettore \(\vec{b}_2\) non è adimenisonale, e ha modulo \(|\vec{b}_2| = r\). La base fisica - già introdotto nel capitolo sulla geometrica analitica todo link - è quindi

\[\begin{split}\begin{cases} \hat{r} = \hat{b}_1 = \cos \theta \hat{x} + \sin \theta \hat{y} \\ \hat{\theta} = \frac{\hat{b}_2}{|\vec{b}_2|} = - \sin \theta \hat{x} + \cos \theta \hat{y} \\ \end{cases}\end{split}\]

Example 28.8 (Spazio \(E^3\): coordinate cartesiane)

I vettori della base naturale sono

\[\begin{split}\begin{cases} \vec{b}_1 = \frac{\partial \vec{r}}{\partial x} = \frac{\partial }{\partial x} \left( x \hat{x} + y \hat{y} + z \hat{z} \right) = \hat{x} \\ \vec{b}_2 = \frac{\partial \vec{r}}{\partial y} = \frac{\partial }{\partial y} \left( x \hat{x} + y \hat{y} + z \hat{z} \right) = \hat{y} \\ \vec{b}_3 = \frac{\partial \vec{r}}{\partial z} = \frac{\partial }{\partial z} \left( x \hat{x} + y \hat{y} + z \hat{z} \right) = \hat{z} \\ \end{cases}\end{split}\]

Ricordando le proprietà dei vettori di una base cartesiana todo link, è immediato verificare che la base naturale di un sistema di coordinate cartesiane è anche la sua base fisica (adimensionale non-dimensionale).

Example 28.9 (Spazio \(E^3\): coordinate cilindriche)

I vettori della base naturale sono

\[\begin{split}\begin{cases} \vec{b}_1 = \frac{\partial \vec{r}}{\partial r } = \frac{\partial }{\partial r } \left( r \cos \theta \hat{x} + r \sin \theta \hat{y} + z \hat{z} \right) = \cos \theta \hat{x} + \sin \theta \hat{y} \\ \vec{b}_2 = \frac{\partial \vec{r}}{\partial \theta} = \frac{\partial }{\partial \theta} \left( r \cos \theta \hat{x} + r \sin \theta \hat{y} + z \hat{z} \right) = -r\sin \theta \hat{x} + r \cos \theta\hat{y} \\ \vec{b}_3 = \frac{\partial \vec{r}}{\partial z } = \frac{\partial }{\partial z } \left( r \cos \theta \hat{x} + r \sin \theta \hat{y} + z \hat{z} \right) = \hat{z} \\ \end{cases}\end{split}\]

E” semplice dimostrare che i tre vettori sono ortogonali, ma il vettore \(\vec{b}_2\) non è adimenisonale, e ha modulo \(|\vec{b}_2| = r\). La base fisica - già introdotto nel capitolo sulla geometrica analitica todo link - è quindi

\[\begin{split}\begin{cases} \hat{r} = \hat{b}_1 = \cos \theta \hat{x} + \sin \theta \hat{y} \\ \hat{\theta} = \frac{\hat{b}_2}{|\vec{b}_2|} = - \sin \theta \hat{x} + \cos \theta \hat{y} \\ \hat{z} = \hat{b}_3 = \hat{z} \\ \end{cases}\end{split}\]

Example 28.10 (Spazio \(E^3\): coordinate sferiche)

I vettori della base naturale sono

\[\begin{split}\begin{cases} \vec{b}_1 = \frac{\partial \vec{r}}{\partial R } = \frac{\partial }{\partial R } \left( R \, \sin \phi \, \cos \theta \, \hat{x} + R \, \sin \phi \, \sin \theta \, \hat{y} + R \, \cos \phi \hat{z} \right) = \sin \phi \, \cos \theta \, \hat{x} + \sin \phi \, \sin \theta \, \hat{y} + \cos \phi \hat{z} \\ \vec{b}_2 = \frac{\partial \vec{r}}{\partial \phi } = \frac{\partial }{\partial \phi } \left( R \, \sin \phi \, \cos \theta \, \hat{x} + R \, \sin \phi \, \sin \theta \, \hat{y} + R \, \cos \phi \hat{z} \right) = R \, \cos \phi \, \cos \theta \, \hat{x} + R \, \cos \phi \, \sin \theta \, \hat{y} - R \, \sin \phi \hat{z} \\ \vec{b}_3 = \frac{\partial \vec{r}}{\partial \theta} = \frac{\partial }{\partial \theta} \left( R \, \sin \phi \, \cos \theta \, \hat{x} + R \, \sin \phi \, \sin \theta \, \hat{y} + R \, \cos \phi \hat{z} \right) = - R \, \sin \phi \, \sin \theta \, \hat{x} + R \, \sin \phi \, \cos \theta \, \hat{y} \end{cases}\end{split}\]

E” semplice dimostrare che i tre vettori sono ortogonali, ma i vettori \(\vec{b}_2\), \(\vec{b}_3\) non sono adimenisonale, e hanno modulo \(|\vec{b}_2| = R\) e \(|\vec{b}_3| = R |\sin \phi|\). La base fisica - già introdotto nel capitolo sulla geometrica analitica todo link - è quindi

\[\begin{split}\begin{cases} \hat{r} = \hat{b}_1 = \sin \phi \, \cos \theta \, \hat{x} + \sin \phi \, \sin \theta \, \hat{y} + \cos \phi \hat{z} \\ \hat{\phi } = \frac{\hat{b}_2}{|\vec{b}_2|} = \cos \phi \, \cos \theta \, \hat{x} + \cos \phi \, \sin \theta \, \hat{y} - \sin \phi \hat{z} \\ \hat{\theta} = \frac{\hat{b}_3}{|\vec{b}_3|} =-\sin \theta \, \hat{x} + \cos \theta \, \hat{y} \end{cases}\end{split}\]

28.1.1.2. Curve coordinate

28.1.1.3. Superfici coordinate

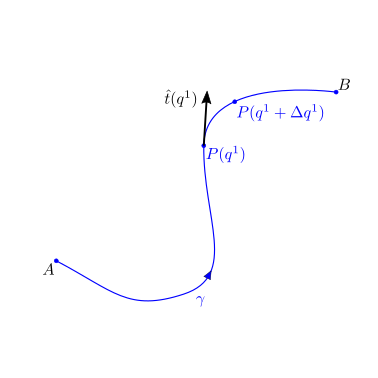
28.1.2. Curve nello spazio

Una curva \(\gamma\) nello spazio può essere rappresentata con la sua equazione parametrica,

\[\gamma: \ \vec{r} = \vec{r}_{\gamma}(q^1) \quad , \quad q^1 \in Q = [q^1_a, q^1_b] \ ,\]

cioè una funzione di una variabile \(q^1\), che associa a ogni valore del parametro \(q^1 \in Q\) il punto \(\vec{r}_\gamma(q^1)\) dello spazio euclideo \(E^n\) appartenente alla curva \(\gamma\).

Una parametrizzazione regolare rappresenta una funzione biunivoca tra i valori della variabile \(q^1\) e i punti nello spazio \(\vec{r}_{\gamma}(q^1)\). Questa condizione si riduce alla condizione che la derivata dei punti della curva rispetto al parametro non sia mai nulla, \(\vec{r}'(q_1) \ne 0\), \(\forall q^{1} \in Q\).

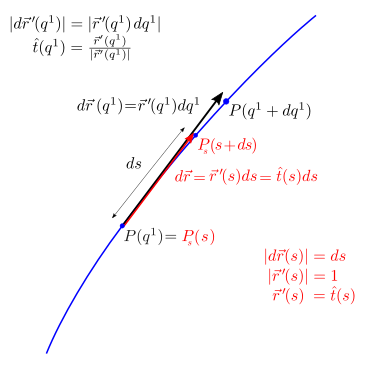
Definition 28.4 (Lunghezza d’arco)

Si definisce lunghezza d’arco il parametro \(s\) che permette la parametrizzazione \(\vec{r}_{\gamma,s}(s)\), \(s \in [s_a, s_b]\) della curva \(\gamma\) tale da avere

\[|\vec{r}'_{\gamma,s}(s)| = 1 \quad , \qquad \forall s \in [s_a, s_b] \ .\]

28.1.2.1. Elemento di curva

La variazione del parametro \(q^1\) produce l’elemento infinitesimo di curva

\[d \vec{r}_{\gamma}(q^1) = \vec{r}'_\gamma(q^1) \, d q^1 \, \]

tangente alla curva e di dimensione (lunghezza)

\[d \ell(q^1) := \left|d \vec{r}_{\gamma}(q^1)\right| = |\vec{r}'_{\gamma}(q^1)| d q^1 \ ,\]

avendo ipotizzato una variazione positiva del parametro \(|d q^1| = d q^1 > 0\) per rimuovere il valore assoluto dalla variazione del parametro. Nel caso si utilizzi il parametro lunghezza d’arco \(s\) Definition 28.4, vale

\[d \ell(s) = |d \vec{r}_{\gamma,s}(s)| = d s \ ,\]

cioè la lunghezza dell’elemento di curva è uguale alla variazione del parametro lunghezza d’arco \(s\). Il vettore \(\vec{r}'_\gamma(s)\) di lunghezza unitaria corrisponde al versore tangente alla curva,

\[\vec{r}'_{\gamma,s}(s) = \hat{t}(s) \ .\]

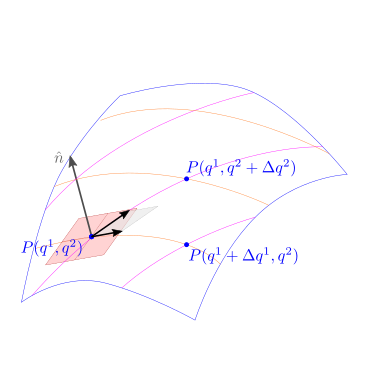
28.1.3. Superfici nello spazio

Una superficie \(S\) nello spazio può essere rappresentata con la sua equazione parametrica,

\[S: \ \vec{r} = \vec{r}_{S}(q^1,q^2) \quad , \quad (q^1,q^2) \in Q \ ,\]

cioè una funzione di due variabili \(q^1\), \(q^2\), che associa a ogni coppia di valori \((q^1, q^2) \in Q\) il punto \(\vec{r}_S(q^1, q^2)\) dello spazio euclideo \(E^n\) appartenente alla superficie \(S\)

Una parametrizzazione regolare rappresenta una funzione biunivoca la coppia di variabili \((q^1, q^2)\) e i punti nello spazio \(\vec{r}_{S}(q^1, q^2)\). Questa condizione equivale alla condizione che…

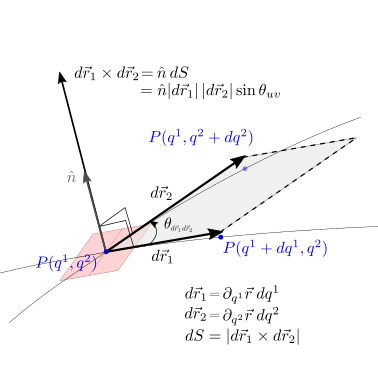
28.1.3.1. Elemento di superficie

La variazione dei parametri \(q^1\) e \(q^2\) produce i vettori infintesimi

\[\begin{split}\begin{aligned} d \vec{r}_1 (q^1,q^2) & = \frac{\partial \vec{r}_S}{\partial q^1}(q^1, q^2) d q^1 \\ d \vec{r}_2 (q^1,q^2) & = \frac{\partial \vec{r}_S}{\partial q^2}(q^1, q^2) d q^2 \\ \end{aligned}\end{split}\]

tangenti alla superficie \(S\). Ricordando il significato geometrico del prodotto vettoriale tra due vettori in spazi euclidei, il prodotto vettoriale \(d \vec{r}_1 \times d \vec{r}_2\) produce un vettore normale alla superficie il cui modulo è uguale all’area \(d S\) del parallelogramma elementare con lati \(d \vec{r}_1\) e \(d \vec{r}_2\),

\[\hat{n} \, dS = d \vec{r}_1 \times d \vec{r}_2 = \frac{\partial \vec{r}_S}{\partial q^1} \times \frac{\partial \vec{r}_S}{\partial q^2} d q^1 d q^2 , \]

avendo ipotizzato una parametrizzazione \(q^1\), \(q^2\) della superficie con la direzione desiderata (orientazione della superficie) del vettore normale \(\hat{n} \, dS\), e sottinteso la dipendenza delle derivate parziali dalle variabili \(q^1\), \(q^2\) per non appesantire la notazione più del dovuto.

28.1.4. Volumi nello spazio

Un volume nello spazio \(E^3\) si può essere rappresentato con una rappresentazione parametrica di \(E^3\),

\[V: \ \vec{r} = \vec{r}_V(q^1, q^2, q^3) \quad , \quad (q^1, q^2, q^3) \in Q \ ,\]

cioè una funzione di tre variabili \(q^1, q^2, q^3\), che associa a ogni triple di valori \((q^1, q^2, q^3) \in Q\) il punto \(\vec{r}_V(q^1, q^2, q^3)\) dello spazio euclideo \(E^n\) appartenente al volume \(V\).

Una parametrizzazione regolare rappresenta una funzione biunivoca la tripla di variabili \((q^1, q^2, q^3)\) e i punti nello spazio \(\vec{r}_{V}(q^1, q^2, q^3)\). Questa condizione equivale alla condizione che…

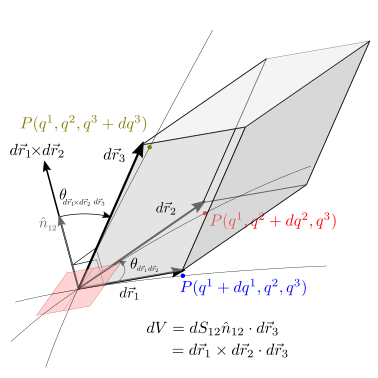
28.1.4.1. Elemento di volume

La variazione dei parametri \(q^1\), \(q^2\) e \(q^3\) produce i vettori infintesimi

\[\begin{split}\begin{aligned} d \vec{r}_1 (q^1,q^2,q^3) & = \frac{\partial \vec{r}_V}{\partial q^1}(q^1, q^2, q^3) d q^1 \\ d \vec{r}_2 (q^1,q^2,q^3) & = \frac{\partial \vec{r}_V}{\partial q^2}(q^1, q^2, q^3) d q^2 \\ d \vec{r}_3 (q^1,q^2,q^3) & = \frac{\partial \vec{r}_V}{\partial q^3}(q^1, q^2, q^3) d q^3 \ . \end{aligned}\end{split}\]

Ricordando il significato geometrico del prodotto misto tra tre vettori in spazi euclidei, il prodotto vettoriale \(d \vec{r}_1 \times d \vec{r}_2 \cdot d \vec{r}_3\) produce uno scalare uguale al volume (con segno) del parallelepipedo elementare con spigoli \(d \vec{r}_1\), \(d \vec{r}_2\), \(d \vec{r}_3\),

\[d V = d \vec{r}_1 \times d \vec{r}_2 \cdot d \vec{r}_3 = \frac{\partial \vec{r}_V}{\partial q^1} \times \frac{\partial \vec{r}_V}{\partial q^2} \cdot \frac{\partial \vec{r}_V}{\partial q^3} d q^1 d q^2 d q^3 , \]

avendo sottinteso la dipendenza delle derivate parziali dalle variabili \(q^1\), \(q^2, q^3\) per non appesantire la notazione più del dovuto.

Example 28.11 (Elemento di volume in coordinate cartesiane)

\[\vec{r} = x \hat{x} + y \hat{y} + z \hat{z}\]

\[\begin{split}\begin{aligned} d V & = \partial_x \vec{r} \cdot \partial_y \vec{r} \times \partial_z \vec{r} \, dx \, dy \, dz = \\ & = \vec{x} \cdot \vec{y} \times \vec{z} \, dx \, dy \, dz = \\ & = \vec{x} \cdot \vec{x} \, dx \, dy \, dz = \\ & = dx \, dy \, dz \ . \end{aligned}\end{split}\]

Example 28.12 (Elemento di volume in coordinate cilindriche)

\[\begin{aligned} \vec{r} & = R \, \cos \theta \, \hat{x} + R \, \sin \theta \, \hat{y} + z \, \hat{z} \end{aligned}\]

\[\begin{split}\begin{aligned} d V & = \partial_R \vec{r} \cdot \partial_{\theta} \vec{r} \times \partial_{z} \vec{r} \, dR \, d\theta \, d z = \\ & = (\cos \theta \, \hat{x} + \sin \theta \, \hat{y}) \cdot (-R \sin \theta \, \hat{x} + R \cos \theta \, \hat{y}) \times \hat{z} \, dR \, d\theta \, d z = \\ & = (\cos \theta \, \hat{x} + \sin \theta \, \hat{y}) \cdot ( R \sin \theta \, \hat{y} + R \cos \theta \, \hat{x}) \, dR \, d\theta \, d z = \\ & = R (\cos^2 \theta + \sin^2 \theta) \, dR \, d\theta \, d z = \\ & = R \, dR \, d \theta \, dz \end{aligned}\end{split}\]

Example 28.13 (Elemento di volume in coordinate sferiche)

\[\begin{aligned} \vec{r} & = r \sin \phi \, \cos \theta \, \hat{x} + r \sin \phi \, \sin \theta \, \hat{y} + r \cos \phi \, \hat{z} \end{aligned}\]

\[\begin{split}\begin{aligned} d V & = \partial_r \vec{r} \cdot \partial_{\phi} \vec{r} \times \partial_{\theta} \vec{r} \, dr \, d\phi \, d\theta = \\ & = (\sin \phi \, \cos \theta \, \hat{x} + \sin \phi \, \sin \theta \, \hat{y} + \cos \phi \, \hat{z} ) \cdot ( r \cos \phi \, \cos \theta \, \hat{x} + r \cos \phi \, \sin \theta \, \hat{y} - r \sin \phi \, \hat{z} ) \times (-r \sin \phi \sin \theta \hat{x} + r \sin \phi \cos \theta \hat{y}) \, dr \, d\phi \, d\theta = \\ & = \dots = \\ & = r^2 \sin \phi \, dr \, d\phi \, d\theta \ . \end{aligned}\end{split}\]

---

1(1,2,3)

Questa rappresentazione può risultare utile quando è necessario svolgere derivate della posizione, poiché i vettori della base cartesiana sono costanti in tutto lo spazio e quindi la loro derivata è nulla. todo Aggiungere collegamenti a sezione derivate (esempi?) e alla cinematica in meccanica classica.