13.2. Piani nello spazio#
Per Euclide, il concetto di piano è un ente geometrico fondamentale della geometria. In geometria analitica, per trovare l’equazione di un piano si possono usare diverse definizioni equivalenti.
13.2.1. Definizioni ed equazione#
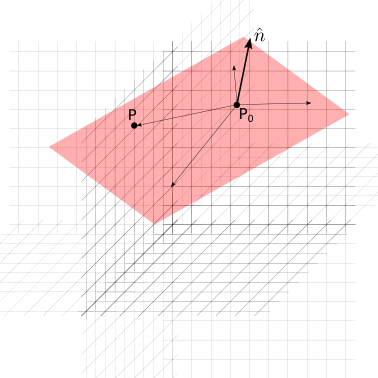
Definizione 1 - Passaggio per un punto e direzione normale. Un piano \(\pi\) può essere definito come il luogo dei punti \(P\) dello spazio che formano un vettore \((P-Q)\) con un punto dato \(Q\) ortogonali a un vettore \(\overrightarrow{n}\) che indica la direzione normale al piano \(\pi\). Usando le proprietà del prodotto scalare,
Usando un sistema di coordinate cartesiane, si può trovare l’equazione implicita del piano \(\pi\),
Osservazione. L’equazione implicita del piano è independente dal modulo del vettore \(\vec{n}\), poiché rappresenterebbe un ininfluente fattore moltiplicativo (diverso da zero) nel termine di sinistra quando uguagliato a zero.
Definizione 2. - Passaggio per un punto e direzioni tangenti. Partendo dalla prima definizione, si possono ricavare le equazioni parametriche del piano. Dato il vettore \(\vec{n}\), si possono trovare due vettori \(\vec{t}_1\), \(\vec{t}_2\) a esso ortogonali,
Se i due vettori non sono tra di loro allineati, o meglio proporzionali, è possibile descrivere tutti i punti del piano come una loro combinazione lineare
Definizione 3. - Luogo dei punti equidistante da due punti distinti dati. Il luogo dei punti P dello spazio equidistanti da due punti \(P_1\), \(P_2\) dati è il piano identificato dalla condizione
Usando un sistema di coordinate cartesiane per identificare i due punti \(P_1 \equiv (x_1,y_1,z_1)\), \(P_2 \equiv (x_2,y_2,z_2)\), per calcolare (il quadrato del)le distanze,
semplificando i termini \(x^2\), \(y^2\), \(z^2\) e raccogliendo mettendo in evidenza le coordinate \(x\), \(y\), \(z\), si ottiene una rappresentazione implicita della retta,
che può essere riscritta in generale nella forma esplicita,
con ovvio significato dei coefficienti \(a\), \(b\), \(c\), \(d\), e \(a\), \(b\), \(c\) non contemporanemante nulli (altrimenti rimarrebbe l’identità \(0 = 0\), corrispondente alla condizione \(a = x_2 - x_1 = 0\), \(b = y_2 - y_1 = 0\), \(c = z_2 - z_1 = 0\) corrispondente ai due punti \(P_1 \equiv P_2\) coinvidenti).
Osservazione. Confrontando le espressioni (13.2), (13.3) con l’espressione (13.1) della prima definizione, si può riconoscere che il vettore che congiunge i due punti \(P_2 - P_1 = (x_2 - x_1) \hat{x} + (y_2 - y_1) \hat{y} + (z_2 - z_1)\) \hat{z} è allineato al vettore \(\vec{n}\) e ortogonale al piano \(\pi\), e al vettore \(a \hat{x} + b \hat{y} + c \hat{z}\).
13.2.2. Posizioni reciproche#
13.2.2.1. Posizione reciproca di punto e piano#
Un punto \(P\) o appartiene o non appartiene a un piano \(\pi: \ \hat{n} \cdot (P - Q) = 0\). Se appartiene al piano, la distanza tra punto e retta è nulla; se non appartiene al piano, la distanza tra punto e piano può essere calcolata usando le proprietà del prodotto interno in spazi euclidei,
todo figura
13.2.2.2. Posizione reciproca di piani#
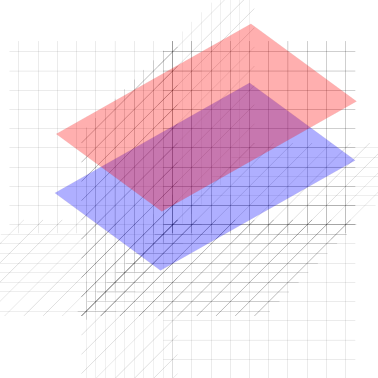
Due piani nello spazio euclideo tridimensionale possono essere:
coincidenti: hanno tutti i punti in comune
paralleli: non hanno nessun punto in comune
incidenti: si intersecano e la loro intersezione definisce una retta
|
|
|