25. Integrali#

25.1. Definizioni#

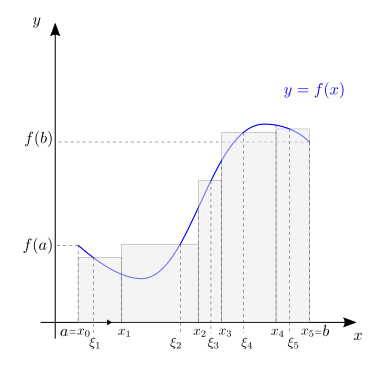
Definition 25.1 (Somma di Riemann)

Data una funzione continua \(f: [a,b] \rightarrow \mathbb{R}\) e una partizione \(P\) dell’intervallo \([a,b]\),

\[P = \{ x_0, x_1, \dots x_n | a = x_0 < x_1 < \dots < x_n = b \} \ ,\]

una somma di Riemann \(\sigma\) della funzione \(f\) sulla partizione \(P\) viene definita come

(25.1)#\[\sigma_P = \sum_{k=1}^{n} f(\xi_k) (x_{k} - x_{k-1}) \ ,\]

con \(\xi_k \in [x_{k-1}, x_k]\).

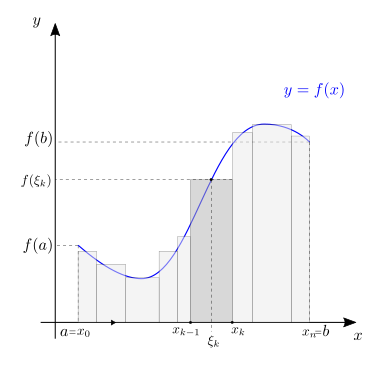
Definition 25.2 (Integrale di Riemann)

Sia \(\Delta x = \max_k (x_{k} - x_{k-1})\), l’integrale definito di Riemann è il limite per \(\Delta x \rightarrow 0\) della somma di Riemann \(\sigma\)

(25.2)#\[\int_a^b f(x) \ dx = \lim_{\Delta x \rightarrow 0} \sigma_P \ .\]

Osservazione. Dato l’intervallo \([a,b]\), per \(\Delta x \rightarrow 0\) il numero di intervalli della partizione tende all’infinito, \(n \rightarrow \infty\).

Definition 25.3 (Funzione integrabile (secondo Riemann))

Una funzione \(f(x): D \subseteq \mathbb{R} \rightarrow \mathbb{R}\) è integrabile sull’intervallo \([a,b] \subseteq D\) se esiste (finito?) l’integrale di Riemann

\[\int_{a}^{b} f(x) \, dx \ .\]

25.1.1. Interpretazione geometrica#

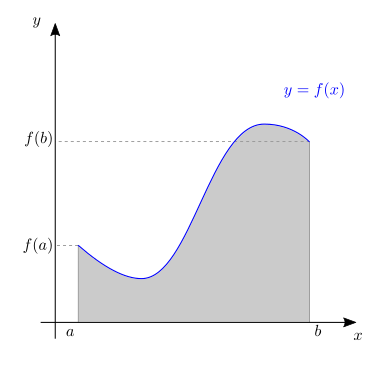
L’integrale definito

\[\int_{a}^{b} f(x) \, dx \ ,\]

corrisponde al valore dell”area con segno tra il grafico della funzione \(y=f(x)\) e l’asse \(x\), per valori di \(x \in [a,b]\). Se la funzione è positiva in un intervallo, il contributo dell’integrale sull’intervallo è positivo; se la funzione è negativa in un intervallo, il contributo dell’integrale sull’intervallo è negativo.

25.1.2. Integrale definito#

25.1.2.1. Proprietà dell’integrale definito#

Dalla definizione (25.2) dell’integrale di Riemann seguono immediatamente le seguenti proprietà:

  • linearità dell’integrale definito

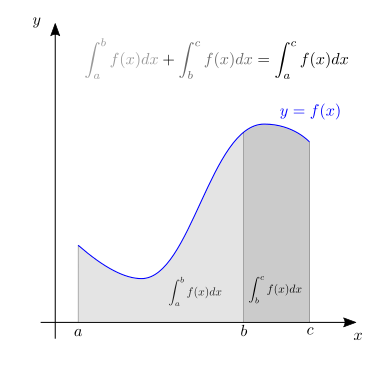
(25.3)#\[\int_a^b \big( \alpha f(x) + \beta g(x) \big) \ dx = \alpha \int_a^b f(x) \ dx + \beta \int_a^b g(x) \ dx \ ,\]

  • additività sull’intervallo

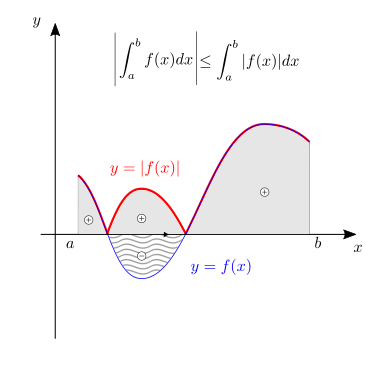
(25.4)#\[\int_a^b f(x) \ dx + \int_b^c f(x) \ dx = \int_a^c f(x) \ dx \ ,\]

  • valore assoluto dell’integrale è minore dell’integrale del valore assoluto

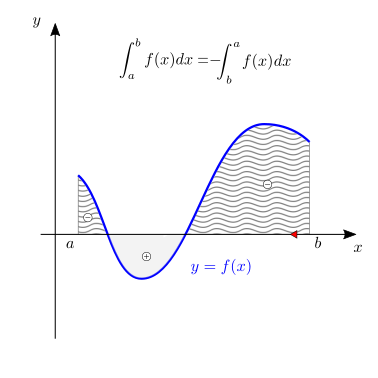
(25.5)#\[\left| \int_a^b f(x) \ dx \right| \le \int_a^b | f(x) | \ dx \ ,\]

  • scambio degli estremi di integrazione

(25.6)#\[\int_{x=a}^{b} f(x) dx = - \int_{x=b}^{a} f(x) \, dx\]

  • integrale di una funzione costante

(25.7)#\[\int_{x=a}^{b} m dx = (b-a) \, m \]

25.1.3. Integrale indefinito#

Usando la proprietà (25.4) di additività sull’intervallo dell’integrale definito,

\[\int_a^x f(t) \ dt = \int_a^b f(t) \ dt + \int_b^x f(t) \ dt \ , \]

si osserva che i due integrali con estremo superiore \(x\) e diverso estremo inferiore differiscono solo per una quantità indipendente da \(x\), \(\int_{a}^{b} f(t) \ dt\). Data la funzione \(f(x)\) e il valore \(a\) come paramtetro, si definisce una funzione di \(x\)

(25.8)#\[F(x;a) := \int_a^x f(t) \ dt \ .\]

Usando questa definizione, è immediato dimostrare che l’integrale definito \(\int_{a}^{b} f(t) \ dt\) è uguale alla differenza della funzione \(F(\cdot; b)\) calcolata nei due estremi,

\[\begin{split}\begin{aligned} \int_{a}^{b} f(t) \ dt & = \int_{c}^{b} f(t) dt + \int_{a}^{c} f(t) dt = \\ & = \int_{c}^{b} f(t) dt - \int_{c}^{a} f(t) dt = \\ & = F(b;c) - F(a;c) \ , \end{aligned}\end{split}\]

e che questo risultato è indipendente dal valore \(c\), usato come parametro nella definizione della funzione \(F\).

Data una funzione \(f(x)\), le due funzioni \(F(x;a_1)\), \(F(x;a_2)\) differiscono solo di un termine che dipende dai parametri \(a_1\), \(a_2\) ma non dalla variabile indipendente \(x\). La famiglia di funzioni \(F(x;a)\) ottenuta per ogni valore di \(a\) definisce quindi una funzione \(F(x)\) a meno di una costante additiva, la funzione primitiva della funzione \(f(x)\).

L”integrale indefinito di una funzione \(f(x)\) viene definito come,

\[\int^x f(t) \ dt = F(x) + C \ ,\]

dove la costante additiva \(C\) tiene conto dell’arbitrarietà appena discussa.

L”integrale definito di una funzione continua \(f(x): D \rightarrow \mathbf{R}\) su un’intervallo \([a,b] \subseteq D\) può quindi essere valutato come la differenza della funzione primitiva \(F(x)\) valutata nell’estremo superiore e nell’estremo inferiore,

\[\int_{x=a}^{b} f(x) \, dx = F(b) - F(a) \ .\]

25.2. Teoremi#

25.2.1. Teorema della media#

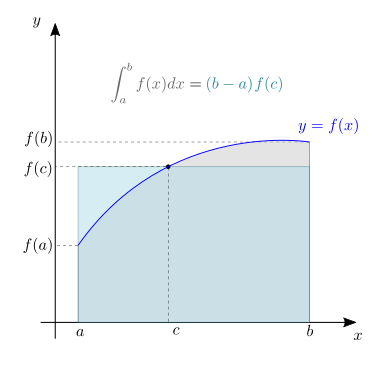
Theorem 25.1 (Teorema della media)

Sia \(f: [a,b] \in \mathbb{R} \rightarrow \mathbb{R}\) una funzione continua su un intervallo \([a,b]\) chiuso e limitato, allora esiste \(c \in [a,b]\) tale che

\[\int_{a}^{b} f(x) dx = (b-a) f(c) \]
Dimostrazione

Poiché \(f(x): [a,b] \rightarrow \mathbb{R}\) è una funzione continua definita su un intervallo chiuso e limitato, allora per il teorema di Weierstrass la funzione ammette minimo \(m\) e massimo \(M\) per valori di \(x \in [a,b]\),

\[m \le f(x) \le M \ .\]

Integrando questa relazione sull’intervallo \([a,b]\),

\[\int_{a}^{b} m \, dx \le \int_{a}^{b} f(x) \, dx \le \int_{a}^{b} M ,\ dx \ .\]

La regola di integrazione per una funzione costante (25.7) permette di calcolare gli integrali estremi

\[(b-a) m \le \int_{a}^{b} f(x) \, dx \le (b-a) M \ ,\]

e dividendo per \((b-a) \ne 0\), si ottiene la relazione

\[m \le \frac{1}{b-a} \int_{a}^{b} f(x) \, dx \le M \ .\]

Siano \(x_m\) e \(x_M \in [a,b]\) i punti - i numeri reali - in cui la funzione assume i valori minimo e massimo. Se \(x_m < x_M\), si applica il teorema dei valori medi sull’intervallo \(I_m = [x_m, x_M]\), in caso contrario sull’intervallo \(I_m = [x_M, x_m]\).

Per il teorema dei valori intermedi, la funzione continua \(f(x)\) definita sull’intervallo chiuso e limitato \(I_m \subseteq [a,b]\), assume tutti i valori compresi tra i valori nei due estremi, cioè esiste un numero \(c \in I_m\) tale che

\[m = f(x_m) \le f(c) \le f(x_M) = M \ ,\]

e tra tutti i valori compresi tra \(m\) e \(M\) esiste un punto \(c\) in cui la funzione assume il valore particolare definito dalla media \(\frac{1}{b-a}\int_{a}^{b} f(x) \, dx\), cioè

\[\exists c \in I_m \subseteq [a,b] \ , \text{ t.c.} \ f(c) = \frac{1}{b-a}\int_{a}^{b} f(x) \, dx \ .\]

25.2.2. Teorema fondamentale del calcolo infinitesimale#

Theorem 25.2 (Teorema fondamentale del calcolo infinitesimale)

Data una funzione \(f: D \rightarrow \mathbb{R}\) integrabile sull’intervallo \([a,b] \subseteq D\), Definition 25.3, si definisce la funzione

\[F(x) := \int_{a}^{x} f(t) \, dt \ .\]

Oss. Qui la variabile di integrazione \(t\) è una variabile dummy, non ha un significato particolare che resista all’operazione di integrazione. La funzione \(F\) ha come argomento \(x\) l’estremo di integrazione superiore dell’integrale.

  1. Se \(f\) è limitata la funzione \(F(x)\) è continua se \(f\) limitata

  2. Se \(f\) è continua in \((a,b)\), allora \(F(x)\) è differenziabile in \((a,b)\) e la sua derivata vale \(F'(x) = f(x)\), o più esplicitamente

    \[\dfrac{d}{dx} \int_{a}^{x} f(t) dt = f(x) \ .\]
Dimostrazione

Continuità. Si dimostra la continuità di \(F(x)\), usando la definizione di funzione continua, valutando \(\lim_{x \rightarrow x_0} F(x)\), e verificando che vale \(\lim_{x \rightarrow x_0} F(x) = F(x_0)\)

\[\begin{split}\begin{aligned} \lim_{x \rightarrow x_0} F(x) & = \lim_{x \rightarrow x_0} \int_{a}^{x} f(t) \, dt = && (1) \\ & = \lim_{x \rightarrow x_0} \left[ \int_{a}^{x_0} f(t) \, dt + \int_{x_0}^{x} f(t) \, dt \right] = && (2) \\ & = \int_{a}^{x_0} f(t) \, dt + \lim_{x \rightarrow x_0} \int_{x_0}^{x} f(t) \, dt = && (3) \\ & = \int_{a}^{x_0} f(t) \, dt = F(x_0) \ , \end{aligned}\end{split}\]

avendo usato (1) l’additività dell’integrale sull’intervallo (25.4), (2) le operazioni con i limiti per scrivere il limite della somma di funzione come la somma dei limiti - almeno, quando i limiti esistono finiti, come in questo caso per l’intergabilità della funzione -, e (3) riconoscendo che l’integrale di una funzione limitata su un intervallo di dimensione nulla è nullo esso stesso.

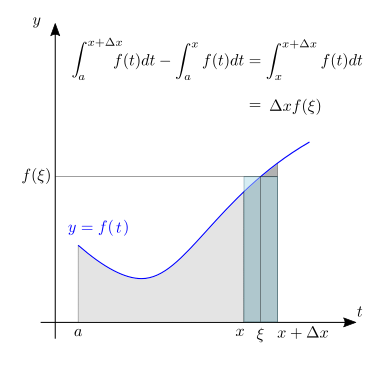
Derivata di \(F(x)\). L’espressione della derivata di \(F(x)\) si ottiene dal calcolo diretto, partendo dalla definizione di derivata di una funzione reale a variabile reale

\[\begin{split}\begin{aligned} F'(x) & := \dfrac{d}{dx} \int_{a}^x f(t) dt = \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ \int_{a}^{x+\varepsilon} f(t) dt - \int_{a}^{x} f(t) dt \Big] = && (1) \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ \int_{x}^{x+\varepsilon} f(y) dy \Big] = && (2) \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \varepsilon f(\xi_{[x,x+\varepsilon]}) = \qquad \xi_{[x,x+\varepsilon]} \in [x,x+\varepsilon] && (3) \\ & = \lim_{\varepsilon \rightarrow 0 } f(\xi_{[x,x+\varepsilon]}) = f(x) . \\ \end{aligned}\end{split}\]

avendo usato (1) l’additività dell’integrale sull’intervallo (25.4), (2) il teorema della media, e (3) la continuità di \(f\), che permette di scrivere

\[\lim_{\varepsilon \rightarrow 0} f(\xi_{[x,x+\varepsilon]}) = \lim_{\xi_{[x,x+\varepsilon]} \rightarrow x} f(\xi_{[x,x+\varepsilon]}) = f(x) \ ,\]

quando \(\xi_{[x,x+\varepsilon]} \rightarrow x\) quando le dimensioni dell’intervallo vengono fatte tendere a zero, e di concludere la dimostrazione del teorema.

Oss. Per evitare questioni sull’appartenenza di \(x + \varepsilon \in [a,b]\) si può usare la definizione «all’indietro» della derivata,

\[F'(x) := \lim_{\varepsilon \rightarrow 0} \frac{f(x) - f(x-\varepsilon)}{\varepsilon} \ . \]

25.2.3. Derivata su dominio dipendente dalla variabile indipendente#

Theorem 25.3 (Derivata su dominio dipendente dalla variabile indipendente - Reynolds)

Sia \(x \in D\), e gli estremi di integrazione \(a(x)\), \(b(x)\) todo Caratteristiche?

\[\dfrac{d}{dx} \int_{a(x)}^{b(x)} f(t) \, dt = - a'(x) \, f(a(x)) + b'(x) f(b(x)) \]
Dimostrazione
\[\begin{split}\begin{aligned} \dfrac{d}{dx} \int_{a(x)}^{b(x)} f(y) dy & = \lim_{\varepsilon \rightarrow 0 }\frac{1}{\varepsilon} \Big[ \int_{a(x+\varepsilon)}^{b(x+\varepsilon)} f(y) dy - \int_{a(x)}^{b(x)} f(y) dy \Big] = \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ \int_{a(x)}^{b(x)} f(y) dy - \int_{a(x)}^{a(x+\varepsilon)} f(y) dy + \int_{b(x)}^{b(x+\varepsilon)} f(y) dy - \int_{a(x)}^{b(x)} f(y) dy \Big] = \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ - \int_{a(x)}^{a(x+\varepsilon)} f(y) dy + \int_{b(x)}^{b(x+\varepsilon)} f(y) dy \Big] = \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ - ( a(x+\varepsilon) - a(x) ) f(\alpha) + ( b(x+\varepsilon) - b(x) ) f(\beta) \Big] = \qquad \alpha \in [a(x), a(x+\varepsilon)] \ , \quad \beta \in [b(x), b(x+\varepsilon)] \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ - ( \varepsilon a'(x) + o(\varepsilon) ) f(\alpha) + ( \varepsilon b'(x) + o(\varepsilon) ) f(\beta) \Big] = \\ & = \lim_{\varepsilon \rightarrow 0 } \frac{1}{\varepsilon} \Big[ - \varepsilon a'(x) \, f(\alpha) + \varepsilon b'(x) \, f(\beta) \Big] = \\ & = \lim_{\varepsilon \rightarrow 0 } \Big[ - a'(x) \, f(\alpha) + b'(x) \, f(\beta) \Big] = \\ & = - a'(x) \, f(a(x)) + b'(x) \, f(b(x)) \ . \end{aligned}\end{split}\]

25.3. Integrali fondamentali#

Una volta dimostrato il teorema fondamentale del calcolo infinitesimale, questo risultato può essere usato per valutare gli integrali fondamentali come l’operazione inversa alla derivazione applicata alle derivate fondamentali

\[\begin{split}\begin{aligned} \int x^n \ dx & = \frac{1}{n+1} x^{n+1} + C \qquad (\text{if } n \neq -1) \\ \int e^x \ dx & = e^x + C \\ \int \frac{1}{x} \ dx & = \ln | x | + C \\ \int \cos x \ dx & = \sin x + C \\ \int \sin x \ dx & =-\cos x + C \end{aligned}\end{split}\]

Per un’ulteriore lista si rimanda alla tabella a fine sezione.

25.4. Integrali impropri#

Vengono definiti integrali impropri alcune famiglie di integrali definiti, come ad esempio:

  • gli integrali di funzioni continue definite su domini con almeno un estremo aperto (finito o infinito), \(f: D_{a,b} \subseteq \mathbb{R} \rightarrow\), che hanno come estremo di integrazione un estremo dell’intervallo. Questo caso comprende sia i limiti al finito

Example 25.3 (\(\int_{a}^{+\infty} \frac{1}{n^n}\))

…

25.4.1. Condizioni di integrabilità#

…

25.4.2. Valore principale di Cauchy#

In alcuni casi è possibile «risolvere» una forma indeterminata della forma \(+\infty - \infty\) nel calcolo di un integrale improprio che dà come risultato un valore finito. Questo valore finito viene definito valore principale di Cauchy. E” questo l’esempio dell’integrale della funzione \(\frac{1}{x}\) su un intervallo che contiene il punto \(x=0\). Questo punto è un punto di discontinuità della funzione, dove questa non è definita. Dati due valori \(a\), \(b\) tali che \(a < 0 < b\), l’integrale \(\int_{x=a}^{b} \frac{1}{x} \, dx\) viene quindi interpretato come

\[\int_{x=a}^{b} \frac{1}{x} \, dx = \lim_{c \rightarrow 0^+} \left[ \int_{a}^{-c} \frac{1}{x} + \int_{c}^{b} \frac{1}{x} \, dx \right] \ ,\]

e il suo calcolo produce il risultato

\[\begin{split}\begin{aligned} \int_{x=a}^{b} \frac{1}{x} \, dx & = \lim_{c \rightarrow 0^+} \left[ \int_{a}^{-c} \frac{1}{x} + \int_{c}^{b} \frac{1}{x} \, dx \right] = \\ & = \lim_{c \rightarrow 0^+} \left[ \ln|-c| - \ln|a| + \ln |b| - \ln|c| \right] = \\ & = \ln |b| - \ln |a| \ . \end{aligned}\end{split}\]

25.5. Regole di integrazione#

25.5.1. Integrazione per parti#

La regola di integrazione per parti viene ottenuta integrando la regola di derivazione del prodotto (24.6). Siano \(F(x)\), \(G(x)\) le primitive delle funzioni \(f(x)\), \(g(x)\), e quindi vale \(F'(x) = f(x)\), \(G'(x) = g(x)\). La regola di derivazione del prodotto \(F(x)G(x)\) viene scritta come

\[\begin{split}\begin{aligned} (F(x) G(x))' & = F'(x) G(x) + F(x) G'(x) = \\ & = f(x) G(x) + F(x) g(x) \end{aligned}\end{split}\]

Isolando il termine \(f(x)G(x)\) e integrando il primo termine grazie al teorema fondamentale del calcolo infinitesimale, si ottiene

\[\begin{split}\begin{aligned} \int f(x) G(x) dx & = \int \left( F(x) G(x) \right)' dx - \int F(x) g(x) dx = \\ & = F(x) G(x) - \int F(x) g(x) dx \ . \end{aligned}\end{split}\]

Nota

Consigli:

  • \(f(x)\) facile da integrare,…

  • Derivazione che riporti a integrali più semplici: esempio, può ridurre di \(1\) la potenza della funzione \(G(x) = x^n\) a ogni applicazione dell’integrazione per parti

  • …

25.5.2. Integrazione con sostituzione#

La regola di integrazione con sostituzione viene ottenuta dalla regola di derivazione della funzione composta (24.8). Sia \(\widetilde{F}(x)\) la funzione composta \(\widetilde{F}(x) = F( y(x) )\) e siano definite le derivate

\[\widetilde{f}(x) = \dfrac{d}{dx} \widetilde{F}(x) \qquad , \qquad f (y) = \dfrac{d}{dy} F (y)\]

per la regola di derivazione della funzione composta,

\[\widetilde{f}(x) := \dfrac{d}{dx} \widetilde{F}(x) = \dfrac{d}{dx} F(y(x)) = \dfrac{d F}{d y}(y(x)) \frac{d y}{d x}(x) =: f(y(x)) y'(x) \ .\]

Usando il teorema del calcolo infinitesimale, todo

\[\begin{split}\begin{aligned} \widetilde{F}(x) & = \int \widetilde{f}(x) \, dx + C = \\ & = \int f(y(x)) \, \underbrace{ y'(x) \, dx}_{= d y} + C = \\ & = \int f(y) \, dy + C = F(y) \ . \end{aligned}\end{split}\]

25.5.2.1. Sostituzioni utili#

Funzioni trigonometriche e iperboliche.

\[\begin{split}\begin{aligned} & \sqrt{a^2 - x^2} && \rightarrow && x = a \sin \theta \quad \text{ or } \quad x = a \cos \theta \\ & \sqrt{a^2 + x^2} && \rightarrow && x = a \sinh \theta \\ & \sqrt{x^2 - a^2} && \rightarrow && x = a \cosh \theta \\ \end{aligned}\end{split}\]

Radici.

\[\begin{split}\begin{aligned} & \sqrt[n]{ax + b} && \rightarrow && ax + b = z^n \\ & \sqrt{a + bx + x^2} && \rightarrow && a + bx + x^2 = ( z - x )^2 \\ & \sqrt{a + bx - x^2} = \sqrt{(\alpha + x)(\beta - x)} && \rightarrow && a + bx - x^2 = ( \alpha + x )^2 z^2 \\ \end{aligned}\end{split}\]

Tangente \(\frac{x}{2}\) La trasformazione di coordinate

\[z = \tan\left( \frac{x}{2} \right) \ ,\]

risulta utile a trasformare un’integranda dove compaiono funzioni trigonometriche in un’integranda razionale.

25.5.3. Frazioni parziali#

todo E” una regola valida per funzioni integrande che possono essere scritte come il rapporto di due polinomi, \(f(x) = \frac{N(x)}{D(x)}\), e segue direttamente dalla possibilità di scomporre il polinomio a denominatore in polinomi di primo e secondo grado, grazie al teorema fondamentale dell’algebra, e scrivere il rapporto come somma di frazioni.

todo descrivere meglio il metodo

25.6. Applicazioni#

25.6.1. Studio di funzione#

Uno studio di funzione completo può richiedere la padronanza di tutti gli strumenti del calcolo infinitesimale: ricerca del dominio, limiti, derivate e integrali.