12.5. Coniche#
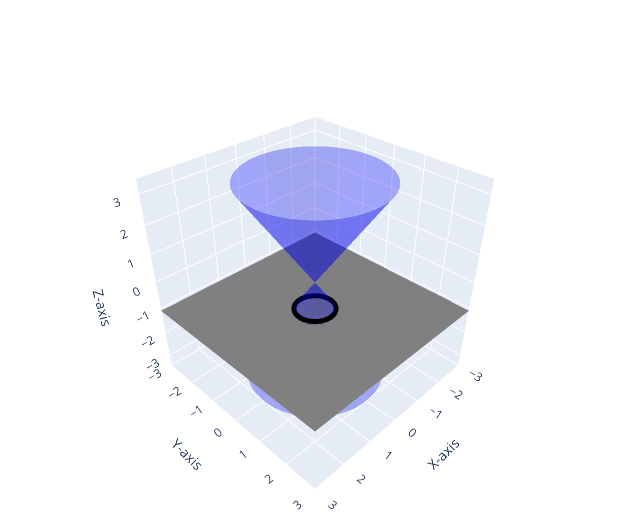
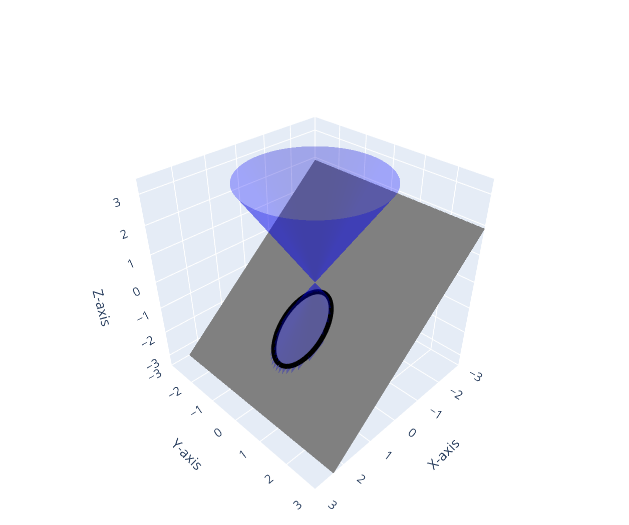
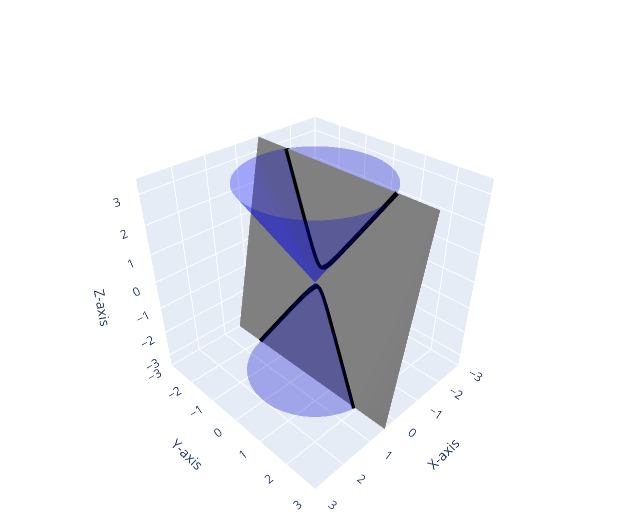
Le coniche sono curve che possono essere ottenute come intersezione tra un piano e un (doppio) cono circolare retto, come dimostrabile con gli strumenti della geometria nello spazio.
Queste curve compaiono in diversi ambiti della matematica e della fisica. Ad esempio,
in geometria: le coniche sono le intersezioni tra un piano e un doppio cono circolare retto; l’inclinazione del piano rispetto all’asse del cono determina il tipo di conica: cerchio, ellisse, parabola o iperbole.
in ottica: le coniche hanno proprietà geometriche che risultano utili in ottica, e nella trasmissione delle informazioni (le antenne paraboliche si chiamano così, poiché hanno la forma di un paraboloide)
in meccanica: le traiettorie di due corpi isolati soggetti alla mutua interazione con intensità inversamente proprozionale al quadrato della loro distanza sono coniche; sono coniche quindi le orbite
di due corpi soggetti a mutua gravitazione in astronomia
di due corpi soggetti a mutua interazione elettrica
Sezioni di cono
|
|
|
|
Proprietà ottiche
Le coniche possono essere definite in maniera implicita, senza fare uso di sistemi di coordinate. Partendo da definizioni implicite equivalenti, e sfruttando l’arbitrarietà nel definire il sistema di coordinate più comodo, vengono ricavate
prima, le equazioni delle coniche in forma canonica con un’opportuna scelta di sistemi di coordinate
poi, l’equazione in forma generale di una conica nel piano, ottenuta tramite una trasformazione rigida - roto-traslazione - della curva o, viceversa, delle coordinate.
Queste curve possono essere definite a partire da un punto \(F\), detto fuoco, e una retta \(d\), detta direttrice come verrà fatto per ricavare le equazioni in coordinate polari delle coniche.
Definizione in termini di eccentricità
Una conica può essere definita come il luogo dei punti \(P\) dello spazio per i quali il rapporto tra la distanza dal fuoco e dalla direttrice è costante,
Questo rapporto viene definito eccentricità della conica e il suo valore determina la figura geometrica descritta:
\(e<1\), ellisse; il caso particolare della circonferenza con eccentricità nulla, con \(\text{dist}(P,d) \rightarrow \infty\)
\(e=1\), parabola;
\(e>1\), iperbole;
Esistono due fuochi e due direttrici per ogni ellisse e ogni iperbole.
E” possibile definire le coniche anche grazie alla proprietà che caratterizza la distanza dei punti della conica dai fuochi, come verrà fatto per trovare le equazioni in coordinate cartesiane delle coniche.
Definizione in termini di distanza dai fuochi
una circonferenza è il luogo dei punti del piano che hanno distanza costante da un punto \(C\),
un’ellisse è il luogo dei punti del piano che hanno la somma delle distanze da due punti dati, i fuochi \(F_1\) e \(F_2\), costante,
\[|P-F_1| + |P-F_2| = 2 \, a \ ,\]una parabola è il luogo dei punti del piano equidistante da un punto \(F\), il fuoco della parabola, e da una retta \(d\), la direttrice
un’iperbole è il luogo dei punti del piano che hanno la differenza delle distanze da due punti dati, i fuochi \(F_1\) e \(F_2\), costante,
\[|P-F_1| - |P-F_2| = 2 \, a \ ,\]avendo considerato il modulo delle distanze per comprendere entrambi i rami dell’iperbole