7.2. Spazio vettoriale euclideo

Definizione di uno spazio vettoriale euclideo.

todo

7.2.1. Prodotto interno e distanza

Uno spazio vettoriale euclideo può essere equipaggiato con un’operazione bilineare, simmetrica (su campi reali), e semi-definita positiva, definita prodotto interno,

\[\cdot: \ V \times V \rightarrow \mathbb{R} \ ,\]

che permette di definire la norma di un vettore e l’angolo tra due vettori

\[\begin{split}\begin{aligned} \vec{u} \cdot \vec{v} & := |\vec{u}||\vec{v}| \cos \theta_{\vec{u} \vec{v}} \\ |\vec{v}| & = \sqrt{\vec{v} \cdot \vec{v}} \\ \end{aligned}\end{split}\]

E” semplice verificare che la definizione di un prodotto interno induce la definizione di una norma. Infatti, calcolando il prodotto interno tra un vettore \(\vec{v}\) e se stesso, l’angolo compreso è l’angolo nullo, \(\theta_{\vec{v} \vec{v}} = 0\), con \(\cos \theta_{\vec{u}\vec{u}} = 0\).

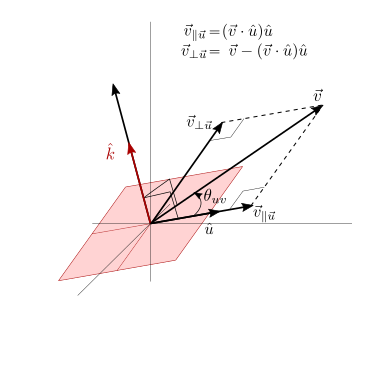
Il prodotto scalare risulta utile anche nella definizione di operazioni di proiezione. Ad esempio, la proiezione ortogonale di un vettore \(\vec{v}\) lungo la direzione identificata dal vettore unitario \(\hat{u}\) è il vettore

\[\vec{v}_{\parallel \hat{u}} = \hat{u} \left( \hat{u} \cdot \vec{v} \right) \ ,\]

che ha la stessa direzione di \(\hat{u}\) e modulo uguale alla proiezione ortogonale di \(\vec{v}\) su di esso, \(\hat{u} \cdot \vec{v}\). La proiezione del vettore \(\vec{v}\) in direzione ortogonale a quella indicata da \(\hat{u}\) si può ottenere per differenza e quindi

\[\begin{split}\begin{aligned} \vec{v}_{\perp \hat{u}} & = \vec{v} - \vec{v}_{\parallel \hat{u}} = \\ & = \vec{v} - \hat{u} \left( \hat{u} \cdot \vec{v} \right) = \\ & = \left[ \hat{I} - \hat{u} \otimes \hat{u} \right] \cdot \vec{v} \ . \\ \end{aligned}\end{split}\]

dove ci si è concessi la licenza poetica di introdurre nell’ultima riga il tensore di proiezione ortogonale in direzione perpendicolare a \(\hat{u}\),

\[\mathbb{P}_{\perp \hat{u}} = \mathbb{I} - \hat{u} \otimes \hat{u} \ ,\]

rappresentazione astratta (vettoriale/tensoriale, che non dipende dalla scelta di una base vettoriale) della trasformazione già mostrata in algebra lineare todo aggiungere riferimento agli esercizi di algebra lineare sulle proiezioni

todo Discutere rappresentazione intrinseca/astratta/vettoriale e per coordinate.

7.2.2. Prodotto vettoriale

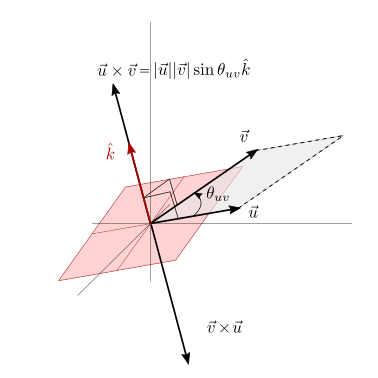
Per lo spazio euclideo \(E^3\) è possibile definire anche un’operazione bilineare, antisimmetrica, definita prodotto vettoriale,

\[\times: \ V \times V \rightarrow V \ ,\]

in modo tale da avere

\[\vec{u} \times \vec{v} = \hat{k} |\vec{u}| |\vec{v}| \sin \theta_{\vec{u} \vec{v}} \ ,\]

con il vettore \(\hat{k}\) ortogonale a entrambi i vettori \(\vec{u}\), \(\vec{v}\) nella direzione definita dalla regola della mano destra todo

• todo. E in \(E^2\)? A volte è comodo assumere che esista una dimensione aggiuntiva, e che quindi ci si trovi in \(E^3\). In questo caso, il prodotto vettore di due vettori di \(E^2\) è sempre ortogonale ad esso.

• todo. Il prodotto vettoriale può essere visto come un caso particolare di un’operazione «strana» chiamata prodotto esterno

7.2.3. Prodotto misto

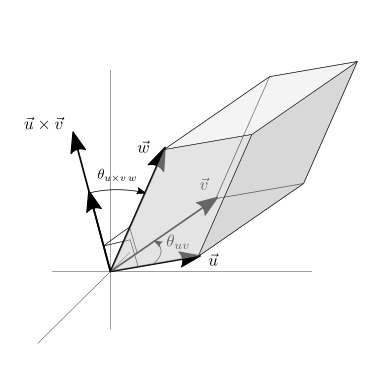
Nello spazio euclideo \(E^3\) si può definire il prodotto misto tra 3 vettori, come il prodotto scalare di uno di questi e il prodotto vettore degli altri due

\[\vec{u} \cdot \vec{v} \times \vec{w} \ .\]

Il prodotto misto ha un significato geometrico evidente: il valore del proodotto misto di tre vettori è uguale al volume del parallelepipedo costruito con i tre vettori come spigolo.

7.2.4. Base cartesiana

In uno spazio vettoriale euclideo, \(E^3\), è possibile definire una base carteisana, \(\{ \hat{x}, \hat{y}, \hat{z} \}\), come un’insieme di vettori di norma unitaria e reciprocamente ortogonali,

\[\begin{split}\begin{aligned} \hat{x} \cdot \hat{x} & = \hat{y} \cdot \hat{y} = \hat{z} \cdot \hat{z} = 1 \\ \hat{x} \cdot \hat{y} & = \hat{y} \cdot \hat{z} = \hat{z} \cdot \hat{x} = 0 \end{aligned}\end{split}\]

e usando il prodotto vettore per definire l’orientazione dei 3 vettori,

\[\begin{split}\begin{aligned} \hat{x} \times \hat{y} & = \hat{z} \\ \hat{y} \times \hat{z} & = \hat{x} \\ \hat{z} \times \hat{x} & = \hat{y} \\ \end{aligned}\end{split}\]

Un vettore di uno spazio vettoriale può essere sempre scritto come combinazione lineare degli elementi di una base vettoriale,

\[\vec{v} = v_x \hat{x} + v_y \hat{y} + v_z \hat{z} \ .\]

Usando una base cartesiana, è immediato ricavare le coordinate cartesiane di un vettore \(\vec{v}\) come il prodotto interno del vettore \(\vec{v}\) per i vettori della base,

\[\begin{split}\begin{aligned} v_x & = \hat{x} \cdot \vec{v} \\ v_y & = \hat{y} \cdot \vec{v} \\ v_z & = \hat{z} \cdot \vec{v} \\ \end{aligned}\end{split}\]

Usando una base cartesiana, si possono scrivere:

• la somma di vettori e la moltiplicazione per uno scalare in componenti,

\[\begin{split}\begin{aligned} \vec{v} + \vec{w} & = (v_x \hat{x} + v_y \hat{y} + v_z \hat{z}) + (w_x \hat{x} + w_y \hat{y} + w_z \hat{z}) = \\ & = (v_x + w_x) \hat{x} + (v_y + w_y) \hat{y} + (v_z + w_z) \hat{z} \\ \\ a \vec{v} & = a (v_x \hat{x} + v_y \hat{y} + v_z \hat{z}) = \\ & = ( a v_x ) \hat{x} + ( a v_y ) \hat{y} + ( a v_z ) \hat{z} \end{aligned}\end{split}\]

• il prodotto interno in termini delle componenti cartesiane dei vettori

\[\begin{split}\begin{aligned} \vec{v} \cdot \vec{w} & = (v_x \hat{x} + v_y \hat{y} + v_z \hat{z}) \cdot (w_x \hat{x} + w_y \hat{y} + w_z \hat{z}) = \\ & = v_x w_x + v_y w_y + v_z w_z \end{aligned}\end{split}\]

• il prodotto vettoriale, in termini del determinante formale

\[\begin{split}\begin{aligned} \vec{v} \times \vec{w} & = (v_x \hat{x} + v_y \hat{y} + v_z \hat{z}) \times (w_x \hat{x} + w_y \hat{y} + w_z \hat{z}) = \\ & = (v_y w_z - v_z w_y) \hat{x} + (v_z w_x - v_x w_z) \hat{y} + (v_x w_y - v_y w_x) \hat{z} = \\ & = \left| \begin{matrix} \hat{x} & \hat{y} & \hat{z} \\ v_x & v_y & v_z \\ w_x & w_y & w_z \end{matrix} \right| \end{aligned}\end{split}\]