17. Trigonometria e funzioni trigonometriche - o armoniche

Non solo triangoli! La trigonometria e le funzioni trigonometriche rappresentano un filo conduttore che attraversa la storia della matematica e della scienza

• la trigonometria nasce attorno al II secolo a.C. come «soluzione del triangolo» nell’ambito della geometria, permettendo di risolvere problemi geometrici e pratici legati alla misura di distanze e superfici, all’astronomia, alla geografia, alla navigazione

• grazie all’opera di Fourier tra il XVII e il XVIII secolo, le funzioni trigonometriche si impongono come elementi fondamentali per l”analisi di fenomeni periodici, come…. Un segnale può infatti essere scomposto come somma di contributi periodici elementari, rappresentabili con l’uso di funzioni trigonometriche, o armoniche (uscendo dall’ambito della geometria dei triangoli triangoli e spostandosi nell’ambito dei segnali periodici): ad esempio, le note musicali percepite dall’orecchio umano sono associate a contributi elementari armonici, cioè contributi che hanno una frequenza definita,…; nel caso poi un problema sia lineare, è possibile usare il principio di sovrapposizione di cause ed effettii (PSCE), per studiare gli effetti prodotti dalle singole cause e poi sommarli (composizione, interferenza,…) per ottenere una soluzione generale.

• il legame con l’esponenziale complesso e le regole di derivazione e integrazione,…rendono le funzioni trigonometriche protagoniste anche nella soluzione di molte equazioni differenziali ordinarie (ODE) di interesse

todo:list Analisi di Fourier

Argomenti e applicazioni

• prime definizioni e relazione fondamentale:

  • geometria del triangolo e della circonferenza,…

• formule di somma e sottrazione:

  • fenomeni ondulatori: interferenza, trasformazione tra rappresentazione in onde stazionarie o in onde viaggianti,…

  • …

17.1. Definizione delle funzioni trigonometriche e relazione fondamentale

17.1.1. Seno e coseno

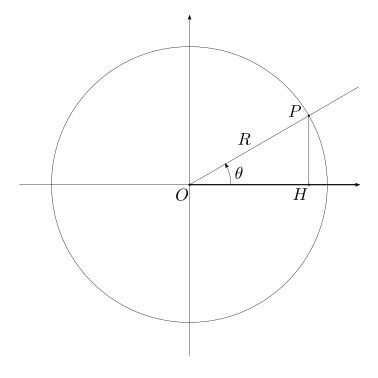
Facendo riferimento a una circonferenza di raggio \(R\), e scegliendo una semiretta di riferimento come origine per la misura degli angoli, positivi in senso orario, si possono definire le funzioni trigonometriche

\[\sin \theta := \frac{\overline{PH}}{R}\]

\[\cos \theta := \frac{\overline{OH}}{R}\]

17.1.2. Relazione fondamentale della trignometria

Usando il teorema di Pitagora è immediato dimostrare la relazione fondamentale della trigonometria tra le funzioni seno e coseno di un angolo,

(17.1)\[\sin^2 \theta + \cos^2 \theta = 1 \ .\]

Notazione.

Nell’uso delle funzioni trigonometriche, \(\sin^2 x\) indica il quadrato della funzione e non la composizione della funzione con se stessa,

\[\sin^2 x = (\sin x)^2 \neq \sin( \sin x) \ .\]

17.1.3. Altre funzioni trigonometriche

Tangente. \(\tan \theta := \dfrac{\sin \theta}{\cos \theta} = \dfrac{\overline{PH}}{\overline{OH}} \ .\)

Cosecante, secante, cotangente. Definizioni al limite tra l’inutile e il dannoso,

\[\begin{split}\begin{aligned} \text{cosec} \ \theta & := \frac{1}{\sin \theta} \\ \text{sec } \ \theta & := \frac{1}{\cos \theta} \\ \text{cotan} \ \theta & := \frac{1}{\tan \theta} \\ \end{aligned}\end{split}\]

17.2. Angoli particolari e proprietà

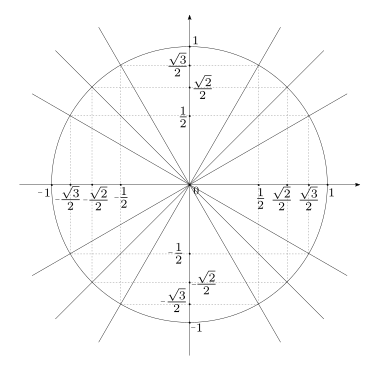
In tabella vengono riportati i valori del seno, coseno e tangente di alcuni angoli particolari \(\theta \in \left[0, \frac{\pi}{2} \right]\)

\(\theta\)	\(\cos \theta\)	\(\sin \theta\)	\(\tan \theta\)
\(0\)	\(1\)	\(0\)	\(0\)
\(\frac{\pi}{6}\)	\(\frac{\sqrt{3}}{2}\)	\(\frac{1}{2}\)	\(\frac{1}{\sqrt{3}}\)
\(\frac{\pi}{4}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(1\)
\(\frac{\pi}{3}\)	\(\frac{1}{2}\)	\(\frac{\sqrt{3}}{2}\)	\(\sqrt{3}\)
\(\frac{\pi}{2}\)	\(0\)	\(1\)	\(\rightarrow \infty\)

Con le proprietà

\[\begin{split}\begin{aligned} \sin x & = - \sin (-x) = - \ \ \cos \left( x + \frac{\pi}{2} \right) = - \sin( x + \pi) \\ \cos x & = \ \ \cos (-x) = - \ \ \sin \left( x + \frac{\pi}{2} \right) = - \cos( x + \pi) \\ \end{aligned}\end{split}\]

è possibile calcolare il valore delle funzioni trigonometriche di angoli particolari nei quattro quadranti.

17.3. Formule di somma e sottrazione

Valgono le seguenti formule per il coseno e il seno della somma e della differenza di angoli,

(17.2)\[\begin{split}\begin{aligned} \cos ( x \mp y ) & = \cos x \ \cos y \pm \sin x \ \sin y && (1) \\ \sin ( x \mp y ) & = \sin x \ \cos y \mp \cos x \ \sin y && (2) \\ \end{aligned}\end{split}\]

Per completezza, come utile esercizio di geometria sulla similitudine dei triangoli, e per familiarizzare con le funzioni armoniche, si fornisce la dimostrazione della formula del coseno della somma.

Dimostrazione di \(\ \cos ( x + y ) = \cos x \ \cos y - \sin x \ \sin y\)

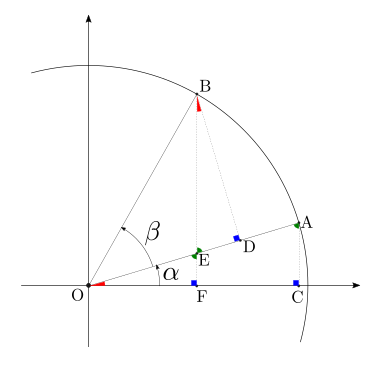
Partendo dall’interpretazione geometrica del coseno di \(\alpha + \beta\),

\[\cos ( \alpha + \beta ) = \frac{\overline{OF}}{R}\]

è necessario esprimere la lunghezza del segmento \(OF\) come multiplo del raggio \(R\).

Usando la similitudine dei triangoli \(OFE\), \(OCA\), e riconoscendo il coseno dell’angolo \(\alpha\),

\[\overline{OF} = \frac{\overline{OC}}{\overline{OA}} \overline{OE} = \cos \alpha \ \overline{OE} \ .\]

La lunghezza del segmento \(OE\) può essere scritta come differenza della lunghezza di \(OD\) e quella di \(ED\); queste ultime due lunghezze possono essere espresse come frazioni del raggio della circonferenza \(R = \overline{OB}\), grazie all’uso delle funzioni trigonometriche e alla similitudine dei triangoli (\(\overline{ED} = \sin \alpha \, \overline{BE} = \sin \alpha \, \frac{\overline{BD}}{\cos \alpha} = \sin \alpha \, \frac{\overline{OB} \sin \beta}{\cos \alpha}\)),

\[\begin{split}\begin{aligned} \overline{OE} = \overline{OD} - \overline{ED} & = \overline{OB} \cos \beta - \overline{OB} \sin \beta \frac{\sin \alpha}{\cos \alpha} = \\ & = R \left( \cos \beta - \overline{OB} \sin \beta \frac{\sin \alpha}{\cos \alpha} \right) \end{aligned}\end{split}\]

Sostituendo questa espressione di \(\overline{OE}\) nell’espressione di \(\overline{OF}\), si ottiene

\[\overline{OF} = \overline{OB} \left( \cos \alpha \cos \beta - \sin \beta \sin \alpha \right)\]

dalla quale si ottiene la relazione desiderata,

\[\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \beta \sin \alpha \ .\]

Example 17.1 (\(\cos(2x) \) e \(\sin(2x)\))

L’espressione di \(\cos(2x)\) e \(\sin(2x)\) possono essere calcolate con le formule (17.2) per le funzioni coseno e seno di unargomento che è somma di due elementi uguali, cioè ponendo \(y = x\). L’espressione di \(\cos(2x)\) può essere riscritta in diverse espressioni usando la relazione fondamentale della trigonometria (17.1),

(17.3)\[\begin{split}\begin{aligned} \cos ( 2x ) & = \cos^2 x - \sin^2 x = \\ & = 2 \cos^2 x - 1 = \\ & = 1 - 2 \sin^2 x \sin ( 2x ) & = 2 \sin x \cos x \\ \end{aligned}\end{split}\]

dato che possono essere utili in parecchie circostanze per riconoscere

(17.4)\[\begin{split}\begin{aligned} \cos^2 x & = \frac{1}{2} \left( 1 + \cos (2x) \right) \\ \sin^2 x & = \frac{1}{2} \left( 1 - \cos (2x) \right) \\ \end{aligned}\end{split}\]

17.4. Werner

\[\begin{split}\begin{aligned} \cos x \cos y & = \dfrac{1}{2} \left[ \cos( x - y ) + \cos ( x + y ) \right] \\ \sin x \sin y & = \dfrac{1}{2} \left[ \cos( x - y ) - \cos ( x + y ) \right] \\ \sin x \cos y & = \dfrac{1}{2} \left[ \sin( x - y ) + \sin ( x + y ) \right] \\ \end{aligned}\end{split}\]

Dimostrazione di \(\ \cos x \cos y = \dfrac{1}{2} \left[ \cos( x - y ) + \cos ( x + y ) \right]\)

Usando le formule del coseno della somma e della sottrazione di una coppia di angoli,

\[\begin{split}\begin{aligned} \cos( x - y ) & = \cos x \cos y + \sin x \sin y \\ \cos( x + y ) & = \cos x \cos y - \sin x \sin y \\ \end{aligned}\end{split}\]

sommando termine a termine si ottiene

\[\cos (x - y) + \cos( x + y ) = 2 \cos x \cos y \ ,\]

dalla quale risulta evidente la relazione desiderata.

17.5. Prostaferesi

Definendo \(p = x-y\) e \(q = x+y\) nelle formule di Werner, è immediato ricavare

\[\begin{split}\begin{aligned} \cos p + \cos q & = 2 \cos\left(\frac{p+q}{2} \right) \cos\left(\frac{q-p}{2} \right) \\ \cos p - \cos q & = 2 \sin\left(\frac{p+q}{2} \right) \sin\left(\frac{q-p}{2} \right) \\ \sin p + \sin q & = 2 \sin\left(\frac{p+q}{2} \right) \cos\left(\frac{q-p}{2} \right) \\ \end{aligned}\end{split}\]

Dimostrazione di \(\ \cos p + \cos q = 2 \cos\left(\frac{p+q}{2} \right) \cos\left(\frac{q-p}{2} \right)\)

Usando la formula di Werner per il prodotto dei coseni,

\[\cos x \cos y = \frac{1}{2} \left[ \cos(x-y) + \cos(x+y) \right]\]

e definendo

\[\begin{split}\begin{cases} x-y = p \\ x+y = q \\ \end{cases} \qquad \rightarrow \qquad \begin{cases} 2 x = p + q \\ 2 y = q - p \\ \end{cases} \qquad \rightarrow \qquad \begin{cases} x = \frac{ p + q }{2} \\ y = \frac{ q - p }{2} \\ \end{cases} \end{split}\]

si ottiene

\[\cos \frac{p+q}{2} \cos\frac{q-p}{2} = \frac{1}{2} \left( \cos p + \cos q \right) \ ,\]

dalla quale è evidente la relazione desiderata.

17.6. Applicazioni utili e frequenti

17.6.1. Combinazione lineare di seno e coseno con stesso argomento

Esempi di utilizzo

• Risposta in frequenza

• Trasformazione da onde viaggianti a onde stazionarie

• …

La combinazione lineare delle funzioni seno e coseno con lo stesso argomento,

\[f(\theta) = A \cos \theta + B \sin \theta \ ,\]

può essere riscritta in termini di una sola funzione armonica, rendendone esplicita l’ampiezza \(F\) e la differenza di fase \(\phi\) rispetto all’argomento \(\theta\),

\[f(\theta) = A \cos \theta + B \sin \theta = F \cos( \theta - \varphi ) \ ,\]

con ampiezza \(F\) e fase \(\varphi\)

\[\begin{split}\begin{aligned} F & = \sqrt{A^2 + B^2} \\ \varphi & \quad \text{ t.c.} \quad \cos \varphi = \frac{A}{F} \ , \quad \sin \varphi = \frac{B}{F} \ . \end{aligned}\end{split}\]

Dimostrazione

Per fare questo, ci si vuole riportare a una delle formule di somma o sottrazione di funzoni trigonometriche. Dai coefficienti \(A\), \(B\) si desidera ricavare due coefficienti che possano essere rispettivamente il coseno e il seno di un angolo \(\varphi\). La relazione fondamentale della trigonometria (17.1) richiede che la somma dei quadrati dei coseno e seno con lo stesso argomento sia uguale a 1. Serve quindi una normalizzazione dei coefficienti, dividendo i coefficienti (e moltiplicando per la stessa quantità diversa da zero per non alterare l’espressione) per la radice quadra della somma dei loro quadrati

\[f(\theta) = \sqrt{A^2+B^2} \left[ \frac{A}{\sqrt{A^2+B^2}} \cos \theta + \frac{B}{\sqrt{A^2+B^2}} \sin \theta \right] \ .\]

E” ora possibile definire un angolo \(\varphi\), il cui coseno e seno sono uguali ai coefficienti,

\[\cos \varphi = \frac{A}{\sqrt{A^2+B^2}} \qquad , \qquad \sin \varphi = \frac{B}{\sqrt{A^2+B^2}} \ , \]

e usare la regola del coseno della differenza (17.2)(1) per poter scrivere

\[\begin{split}\begin{aligned} f(\theta) & = F \left[ \cos \varphi \cos \theta + \sin \phi \sin \theta \right] = \\ & = F \cos ( \theta - \phi ) \ , \end{aligned}\end{split}\]

avendo definito l’ampiezza della funzione armonica \(F = \sqrt{A^2 + B^2}\).

17.6.2.