Algebra sui numeri reali

Contenuti

4. Algebra sui numeri reali#

L’algebra sui numeri reali si occupa delle operazioni fondamentali e delle proprietà dei numeri reali, il cui insieme viene indicato con la lettera $R$ , come anche della risoluzione di equazioni e disequazioni. Dopo la logica e l’insiemistica, l’algebra sui numeri reali è il primo passo in un corso di matematica todo di quale livello?

Questo capitolo ricorda velocmente le operazioni elementari sui numeri reali introdotte nel capitolo sugli insiemi numerici, per poi introdurre con queste le operazioni di potenza, radice e logaritmo. Si fa affidamento sul calcolo letterale, per introdurre i polinomi e alcune loro proprietà che verranno utilizzate per risolvere i problemi algebrici che coinvolgono gli oggetti matematici introdotti: equazioni e disequazioni di un’incognita.

4.1. Operazioni#

Le operazioni elementari sui numeri reali e le loro proprietà sono state introdotte nel capitolo sugli insiemi numerici. Si ricordano le proprietà dell’elevamento a potenza,

a^{b} = c

e le condizioni di esistenza di questa operazione sui numeri reali. Dall’operazione di potenza si introducono le operazioni di radice e di logaritmo chei, sotto le necessarie condizioni, consentono di scrivere

a = \sqrt[b]{c}, b = \log_{a} c .

4.1.1. Potenze#

Nel campo dei numeri reali, l’operazione di potenza, $a^{b} = c$ , è ben definita:

per $a \geq 0$ per ogni $b \in R$
per $a < 0$ solo per $b \in N$

todo controllare, rimandare al capitolo sugli insiemi numerici; spostare nel capitolo sugli insiemi numerici?

4.1.2. Radice#

Definizione e condizioni.

La radice quadrata di un numero reale $a$ è ben definita solo per i numeri reali non negativi, come la soluzione positiva dell’equazione

x^{2} = a^{2},

che in generale ha due soluzioni, $\mp | a |$ , come è immediato verificare con le proprietà delle potenze (o della moltiplicazione),

(- | a |) \cdot (- | a |) = a^{2}, | a | \cdot | a | = a^{2}

Proprietà.

4.1.3. Logaritmo#

Definizione e condizioni.

Proprietà.

4.2. Polinomi#

Scomposizioni elementari.

\begin{array}{r} \begin{aligned} (a + b)^{2} = a^{2} + 2 a b + b^{2} & Quadrato di binomio \\ (a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} & Cubo di binomio \\ (a + b)^{N} = \sum_{n = 1}^{N} (\begin{array}{c} N \\ n \end{array}) a^{N - n} b^{n} & Potenza di binomio \\ a^{2} - b^{2} = (a - b) (a + b) & Differenza di quadrati \\ a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2}) & Differenza di cubi \\ a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2}) & Somma di cubi \\ a^{N} - b^{N} = (a - b) (a^{N - 1} + a^{N - 2} b + \dots + b^{N - 1}) & Differenza di potenze \\ a^{N} + b^{N} = (a + b) (a^{N - 1} - a^{N - 2} b + \dots + b^{N - 1}) & Somma di potenze dispari \end{aligned} \end{array}

todo altre regole? Ruffini?…

4.2.1. Frazioni algebriche#

Una frazione algebrica è il quoziente di due polinomi,

\frac{a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots a_{0}}{b_{m} x^{m} + b_{m - 1} x^{m - 1} + \dots b_{0}} .

Per il teorema fondamentale dell’algebra, ogni polinomio può essere scritto come prodotto di polinomi di primo o secondo ordine. Se i polinomi al numeratore e al denominatore della frazione algebrica non hanno fattori in comune, la frazione algebrica viene definita in forma semplice.

Example 4.1 (Frazioni algebriche semplici e non semplici)

La frazione $\frac{x^{2} - 3 x + 2}{x^{2} + 1} = \frac{(x - 2) (x - 1)}{x^{2} + 1}$ è in forma ridotta, mentre la frazione $\frac{x^{2} - 3 x + 2}{x^{2} - 1} = \frac{(x - 2) (x - 1)}{(x + 1) (x - 1)}$ non è in forma ridotta e, per $x \neq 1$ (!), è uguale a $\frac{x - 2}{x + 1}$ .

Una frazione propria ha il grado $n$ del numeratore inferiore al grado $m$ del denominatore. Una frazione non propria può essere scritta come un polinomio di grado $n - m$ e una frazione propria

Example 4.2 (Frazioni non proprie)

La frazione $\frac{x^{2} + 2 x + 1}{x - 2}$ può essere scritta «completando il quadrato» come

\frac{x^{2} + 2 x + 1}{x - 2} = \frac{x^{2} - 4 x + 4 + 4 x - 4 + 2 x + 1}{x - 2} = \frac{(x - 2)^{2} + 6 x - 3}{x - 2} = x - 2 + 3 \frac{2 x - 1}{x - 2},

con la semplificazione possibile per $x \neq 2$ .

Se il denominatore è scomponibile come prodotto di polinomi, allora la frazione algebrica può essere scritta come somma di frazioni parziali. In alcune applicazioni, come il calcolo degli integrali, può essere conveniente scrivere una frazione come somma di frazioni parziali, poiché risulta più semplice trattare somme di frazioni con numeratore di grado 1 o 2, di frazioni con numeratore di grado qualsiasi.

Example 4.3 (Somma di frazioni parziali)

La frazione $\frac{3 x}{x^{2} - 1}$ può essere scritta come somma di frazioni parziali $\frac{3 x}{x^{2} - 1} = \frac{3}{2} \frac{1}{x - 1} + \frac{3}{2} \frac{1}{x + 1}$ , poiché

\frac{3 x}{x^{2} - 1} = \frac{a}{x + 1} + \frac{b}{x - 1} = \frac{a (x - 1) + b (x + 1)}{x^{2} - 1} = \frac{x (a + b) + b - a}{x^{2} - 1}

\begin{array}{r} {\begin{cases} a + b = 3 \\ b - a = 0 \end{cases} \to a = b = \frac{3}{2} . \end{array}

4.3. Problemi con un’incognita#

4.3.1. Equazioni#

Un’equazione è una relazione di uguaglianza che contiene una o più incognite. L’obiettivo è trovare i valori delle incognite che rendono vera l’uguaglianza.

4.3.1.1. Equazioni di primo grado#

La forma generale di un’equazione di primo grado in un’incognita reale $x \in R$ è

a x + b = 0 a \neq 0

dove la condizione sul coefficiente $a \neq 0$ esclude i casi in cui l’equazione degenera a un’uguaglianza tra parametri. Dopo aver escluso i casi in cui l’equazione degenera in un’uguaglianza tra paramteri, con la condizione $a \neq 0$ , la soluzione generale dell’equazione lineare esiste, è unica ed è

x = - \frac{b}{a} .

Nel caso degenere in cui $a = 0$ , si possono distinguere due casi:

se $b \neq 0$ non esiste nessuna soluzione, poiché l’equazione si riduce alla contraddizione $0 = b \neq 0$ per $\forall x \in R$
se $b = 0$ esistono infinite soluzioni, poiché l’equazione si riduce all”identità $0 = b \neq 0$ per $\forall x \in R$

4.3.1.2. Equazioni di secondo grado#

La forma generale di un’equazione di secondo grado in un’incognita reale $x \in R$ è

a x^{2} + b x + c = 0 a \neq 0,

dove la condizione sul coefficiente $a \neq 0$ esclude i casi in cui l’equazione degenera a un’equazione di primo grado. Le soluzioni dell’equazione vengono cercate completando il quadrato,

0 = x^{2} + \frac{b}{a} x + \frac{b^{2}}{4 a^{2}} - \frac{b^{2}}{4 a^{2}} + \frac{c}{a} = {(x + \frac{b}{2 a})}^{2} - (\frac{b^{2}}{4 a^{2}} - \frac{c}{a}) .

L’equazione viene riscritta come

{(x + \frac{b}{2 a})}^{2} = \frac{b^{2}}{4 a^{2}} - \frac{c}{a},

per mettere in evidenza che l’esistenza delle soluzioni dipende dal valore del discriminante, $\frac{Δ}{(2 a)^{2}} := \frac{b^{2} - 4 a c}{(2 a)^{2}}$ :

se $Δ > 0$ esistono due soluzioni reali distinte, $x_{1, 2} = - \frac{b}{2 a} \mp \frac{\sqrt{Δ}}{2 a} \in R$
se $Δ = 0$ esistono due soluzioni reali coincidenti, $x_{1} = x_{2} = - \frac{b}{2 a} \in R$
se $Δ < 0$ non esistono soluzioni reali, poiché la radice quadra di un numero negativo non è definita nel campo dei numeri reali, $∄ x \in R$

4.3.1.3. Equazioni non lineari generali#

Mentre esiste una formula generale per le equazioni di terzo grado e di quarto grado, queste risultano spesso di scarsa e scarsissima (nulla?) utilità. Per le equazioni polinomiali, a volte è possibile utilizzare i risultati del teorema fondamentale dell’algebra per scrivere il polinomio come prodotto di polinomi di primo e secondo ordine, per i quali è possibile calcolare gli zeri con le formule mostrate nelle sezioni sulle equazioni di primo e secondo grado.

Per equazioni algebriche non lineari che coinvolgono potenze, logaritmi, esponenziali, a parte alcuni casi particolari risolvibili in forma chiusa utilizzando le proprietà di queste operazioni e le soluzioni delle equazioni polinomiali, è necessario affidarsi a metodi di soluzione grafici e/o numerici: todo

m.grafici: soluzione a mano, per guess iniziale di m.numerici
m.numerici: …

4.3.2. Disequazioni#

Un’equazione è una relazione di disuguaglianza che contiene una o più incognite. L’obiettivo è trovare i valori delle incognite che rendono vera la disuguaglianza.

4.4. Rappresentazione grafica di un’equazione con due incognite#

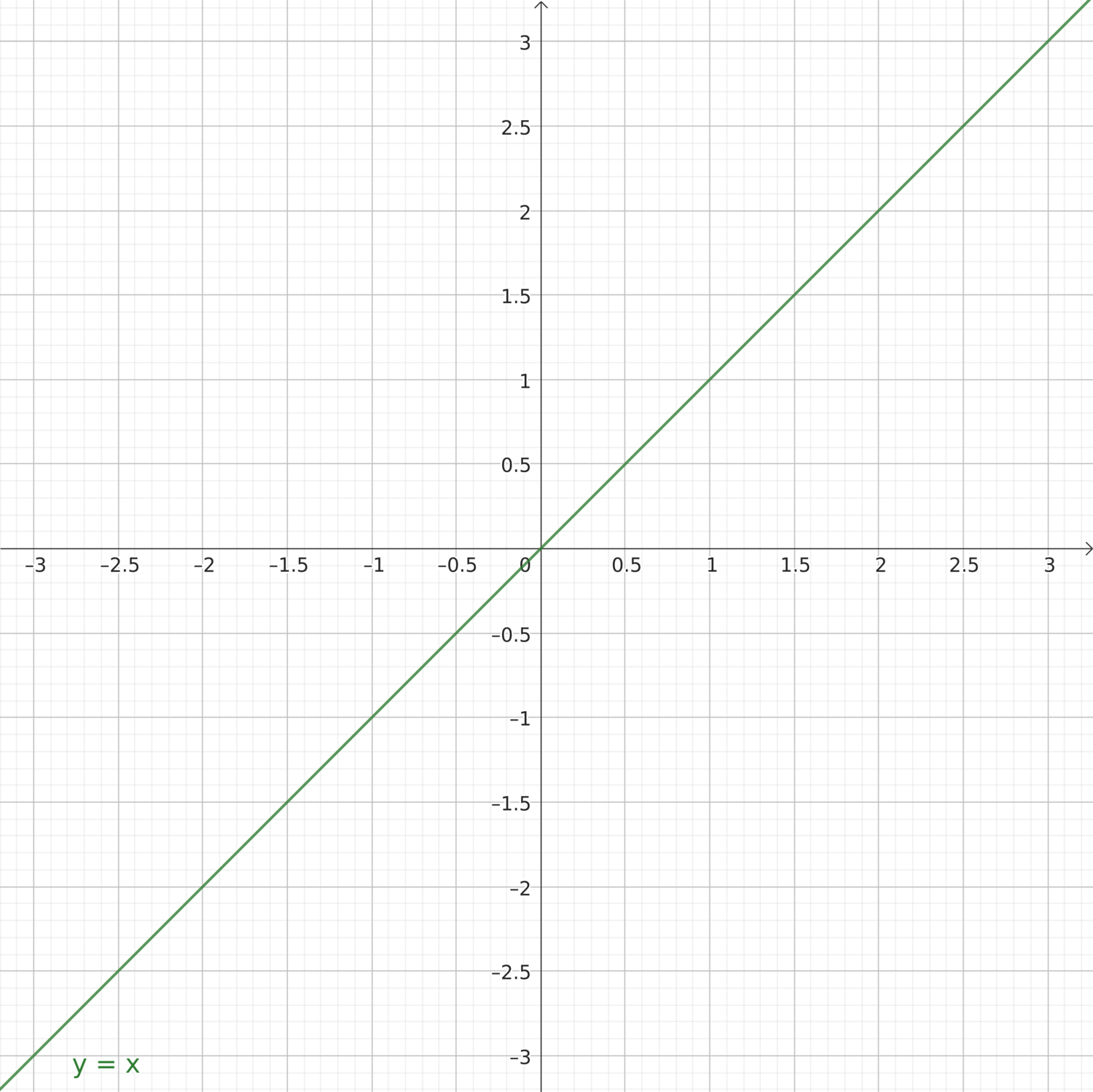
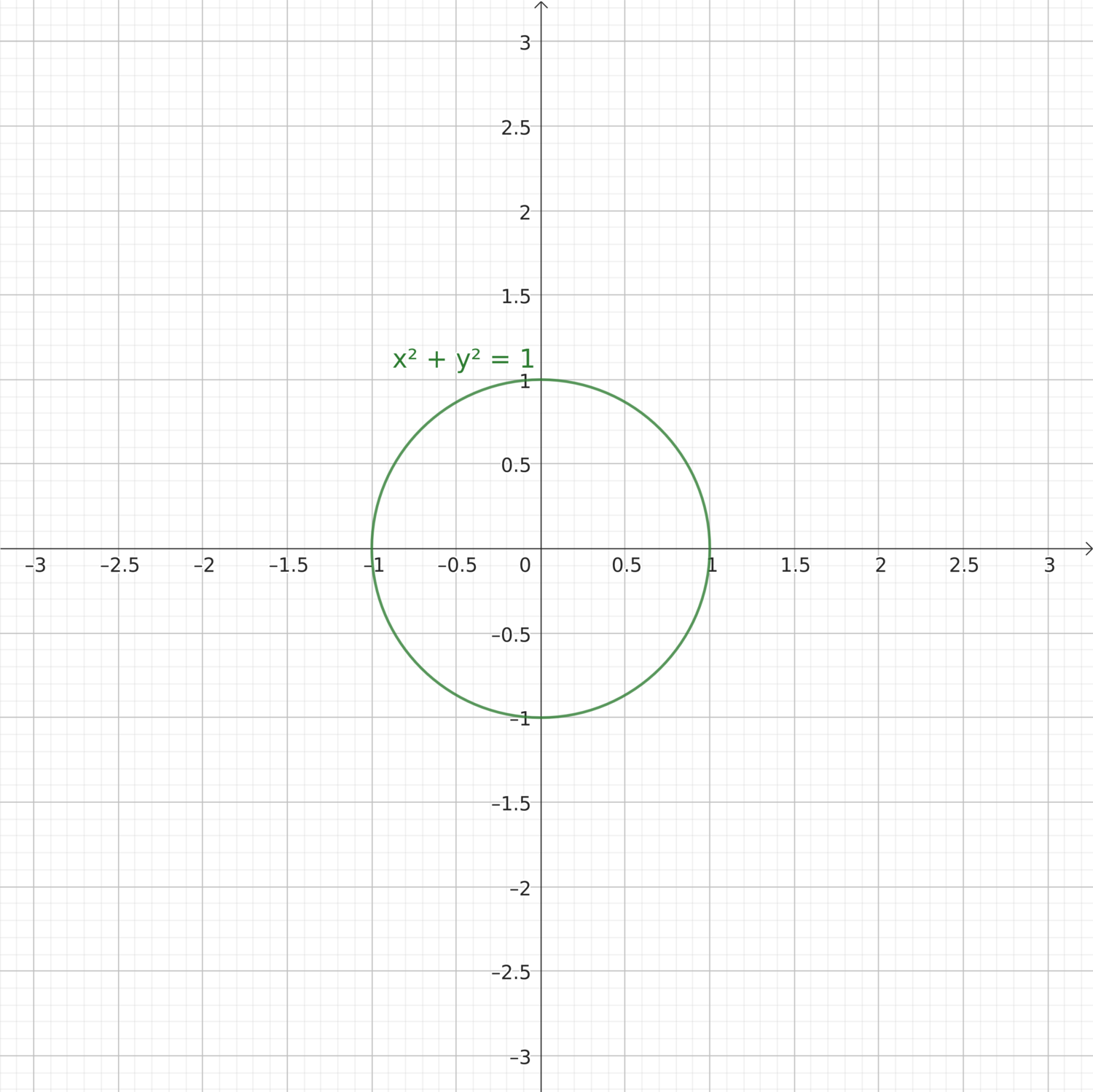
Un’equazione con due incognite $x, y$ è una relazione di uguaglianza che può essere scritta nella forma generale $f (x, y) = 0$ . In generale, a ogni equazione di questa forma può essere associata una curva nel piano, qui descritto dalle coordinate cartesiane $x, y$ . Senza nessuna pretesa di completezza - rimandando per quella alla sezione sulla geometria analitica - qui ci si limita a discutere la rappresentazione grafica nel piano di alcune equazioni elementari

$y = x$ , dipendenza lineare (o proporzionale)
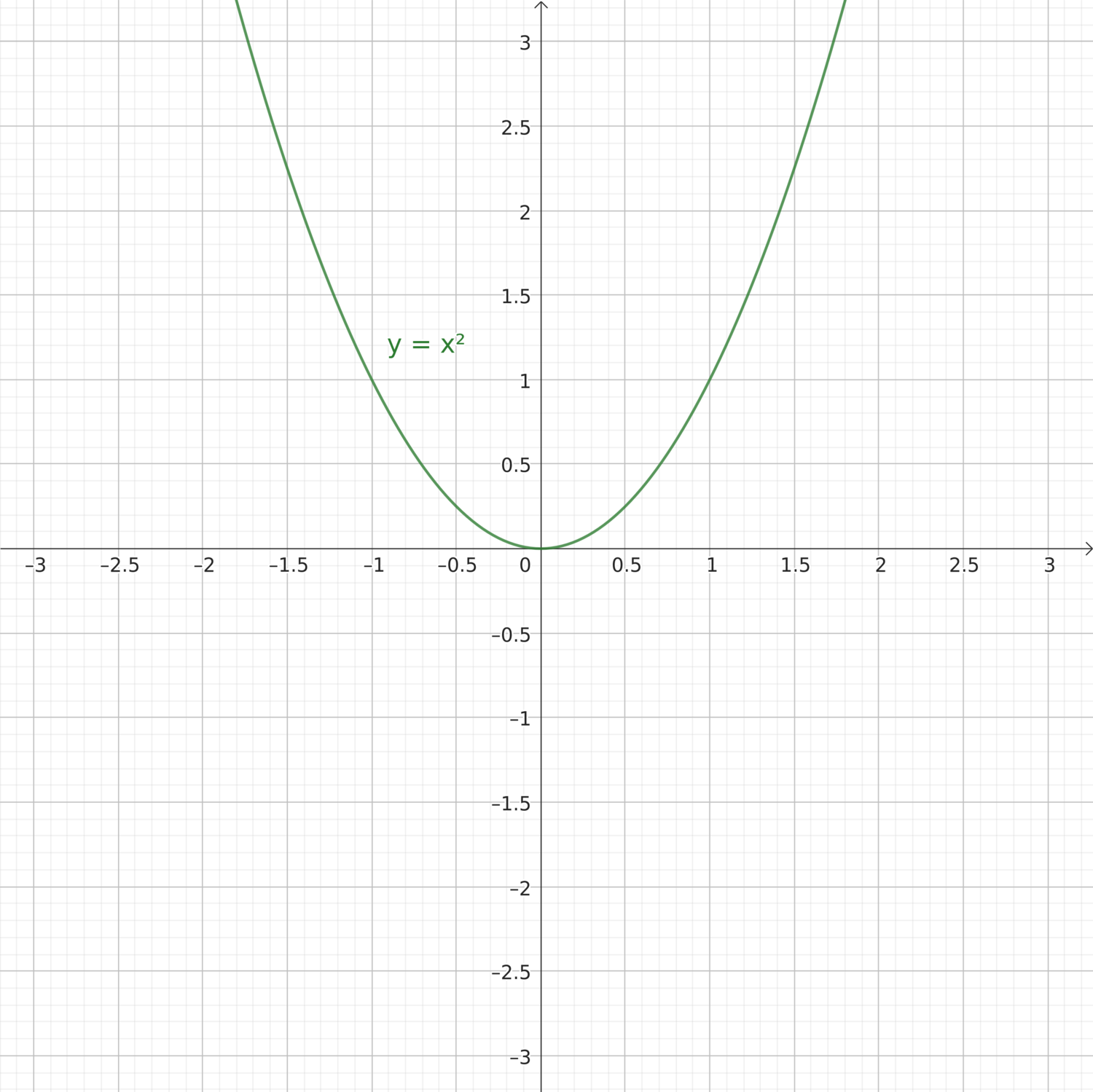
$y = x^{2}$ , dipendenza quadratica
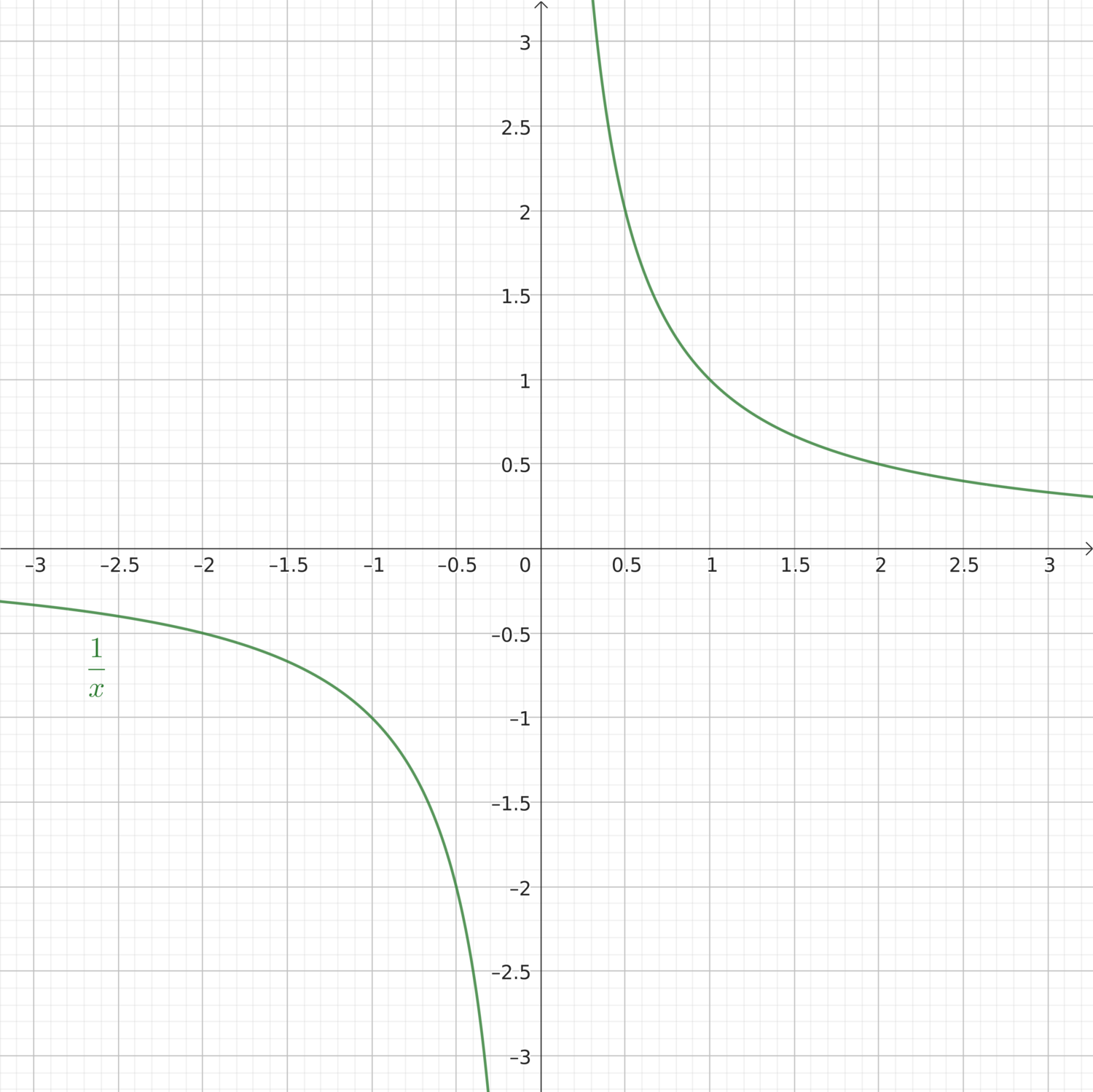
$y = \frac{1}{x}$ , dipendenza inversamente proporzionale
… $y = a^{x}$ , $y = \log_{a} x$ …

e delle equazioni ricavabili da queste con una trasformazione affine di incognite, nella forma

u = \frac{x - x_{0}}{a_{x}}, v = \frac{y - y_{0}}{a_{y}},

x = α_{x} u + x_{0}, y = α_{y} v + y_{0},

corrispondenti alla compsizione di due trasformazioni, in questo ordine:

la scalatura di un fattore $a_{x}$ in direzione $x$ e di un fattore $a_{y}$ in direzione $y$
una traslazione $x_{0}$ in direzione $x$ e di $y_{0}$ in direzione $y$

todo

Aggiungere un’imamgine con il procedimento di trasformazione di variabili/incognite (e coordinate)
Aggiungere un’immagine su alcune famiglie di curve, al variare dei parametri

4.5. Problemi con due o più incognite - sistemi di equazioni e disequazioni#

Un sistema di equazioni è un insieme di equazioni da risolvere simultaneamente. I sistemi di equazioni (e di disequazioni) consentono di introdurre l”algebra su $R^{n}$ , descritta nel capitolo successivo.