24. Derivate#

24.1. Definizione#

Definition 24.1 (Rapporto incrementale)

Il rapporto incrementale di una funzione reale nel punto \(x\) viene definito come il rapporto tra la differenza dei valori della funzione e la differenza del valore della variabile indipendente

(24.1)#\[R[f(\cdot), x, h] := \dfrac{f(x+h)-f(x)}{h} \ .\]

Definition 24.2 (Derivata)

La derivata di una funzione reale in un punto \(x\) viene definita come il limite del rapporto incrementale, per l’incremento della variabile indipendente che tende a zero,

(24.2)#\[f'(x) = \dfrac{d f}{d x}(x) := \lim_{h \rightarrow 0} \dfrac{f(x+h)-f(x)}{h} \ .\]

todo In generale, la derivata di una funzione reale è un’altra funzione reale.

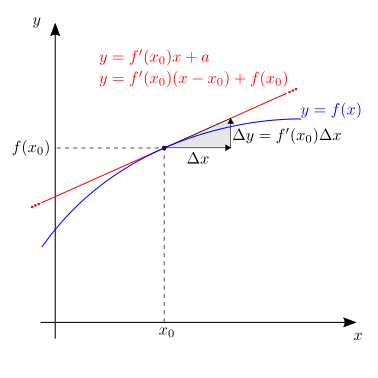
Il limite nella definizione (24.2) della derivata ha la diretta conseguenza di poter scrivere

(24.3)#\[f(x+h) = f(x) + h \, f'(x) + o(h) \ ,\]

cioè un’approssimazione al primo grado in \(h\) di \(f(x+h)\) centrata in \(x\). Per una trattazione più completa delle approssimazioni polinomiali di funzioni, e al ruolo delle derivate in queste, si rimanda alla sezione sulle serie di Taylor e MacLaurin.

24.2. Interpretazione geometrica#

Il valore della derivata di una funzione \(f(x)\) in un punto \(x\) corrisponde al coefficiente angolare della retta tangente alla curva che rappresenta piano cartesiano il grafico della funzione \(y=f(x)\) nel punto di coordinate \((x,f(x))\).

24.3. Incremento di una funzione e differenziale#

Definition 24.3 (Incremento di una funzione)

L’incremento di una funzione \(f\) in seguito all’incremento \(h\) della variabile indipendente \(x\) è

\[\Delta f (x, h) := f(x+h) - f(x) \ .\]

Definition 24.4 (Differenziale di una funzione)

Il differenziale di una funzione \(f\) può essere definito come il termine di primo ordine in \(h\) dell’incremento \(\Delta f(x,h)\),

\[\Delta f(x,h) = d f(x,h) + o(h) \ ,\]

e risulta uguale a

(24.4)#\[d f(x, h) = f'(x) \, h \, .\]

Il confronto con la relazione (24.3) permette di scrivere

\[\Delta f(x,h) = f(x+h) - f(x) = h f'(x) + o(h) \ ,\]

e quindi dimostrare la relazione (24.4) usata per introdurre il concetto di differenziale.

Nota

il differenziale della funzione \(f(x) = x\) è uguale a

\[d x(x,h) = \dfrac{d}{dx} x \, h = h \ ,\]

e quindi si può scrivere nella definizione di differenziale

\[h = dx\]

e quindi

\[d f = f'(x) \, dx \ .\]

24.4. Regole di derivazione#

Usando la definizione (24.2) di derivata e le proprietà dei limiti, è possibile dimostrare le seguenti proprietà

  • linearità

(24.5)#\[\big( a \, f(x) + b \, g(x) \big)' = a \, f'(x) + b \, g'(x)\]

  • derivata del prodotto di funzioni

(24.6)#\[\Bigl( f(x) g(x) \Bigr)' = f'(x) g(x) + f(x) g'(x)\]

  • derivata del rapporto di funzioni

(24.7)#\[\left( \frac{f(x)}{g(x)} \right)' = \frac{f'(x) g(x) - f(x) g'(x)}{g^2(x)}\]
(24.8)#\[\frac{d}{dx} f\big( g(x) \big) = \frac{d f}{dy}\Big|_{y=g(x)} \dfrac{d g}{d x}\Big|_{x}\]
(24.9)#\[ \dfrac{d f^{-1}}{d y}\bigg|_{y = f(x)} = \dfrac{1}{ \dfrac{d y}{d x}\bigg|_{x}} \ .\]
Dimostrazione della linearità dell’operazione di derivazione

La derivata in \(x\) della funzione \(a f(x) + b g(x)\) viene calcolata con la definizione di limite di rapporto incrementale, a \(x\) costante per \(h \rightarrow 0\)

\[\begin{split}\begin{aligned} \left( a f(x) + b g(x) \right)' & = \lim_{h \rightarrow 0} \frac{( a f(x+h) + b g(x+h) ) - ( a f(x) + b g(x) ) }{h} = \\ & = \lim_{h \rightarrow 0} \frac{a ( f(x+h) + f(x) ) + b ( g(x+h) - b g(x) )}{h} = \\ & = a \lim_{h \rightarrow 0} \frac{f(x+h) + f(x)}{h} + b \lim_{h \rightarrow 0} \frac{ g(x+h) - b g(x) }{h} = \\ & = a f'(x) + b g'(x) \ . \end{aligned}\end{split}\]
Dimostrazione della regola del prodotto

La derivata in \(x\) della funzione \(f(x) g(x)\) viene calcolata con la definizione di limite di rapporto incrementale, a \(x\) costante per \(h \rightarrow 0\)

\[\begin{split}\begin{aligned} \left( f(x) g(x) \right)' & = \lim_{h \rightarrow 0} \frac{f(x+h) g(x+h) - f(x) g(x)}{h} = \\ & = \lim_{h \rightarrow 0} \frac{f(x+h) g(x+h) - f(x)g(x+h) + f(x)g(x+h) - f(x) g(x)}{h} = \\ & = \lim_{h \rightarrow 0} \frac{f(x+h) g(x+h) - f(x)g(x+h)}{h} + \lim_{h\rightarrow 0} \frac{f(x)g(x+h) - f(x) g(x)}{h} = \\ & = \lim_{h \rightarrow 0} \underbrace{\frac{f(x+h) - f(x)}{h}}_{\rightarrow f'(x)} \underbrace{g(x+h)}_{\rightarrow g(x)} + f(x) \underbrace{\lim_{h\rightarrow 0} \frac{g(x+h) - g(x)}{h}}_{\rightarrow g'(x)} = \\ & = f'(x) g(x) + f(x) g'(x) \ . \end{aligned}\end{split}\]

todo

Dimostrazione della regola del quoziente

La derivata in \(x\) della funzione \(\frac{f(x)}{g(x)}\) viene calcolata con la definizione di limite di rapporto incrementale, a \(x\) costante per \(h \rightarrow 0\)

\[\begin{split}\begin{aligned} \left( \frac{f(x)}{ g(x)} \right)' & = \lim_{h \rightarrow 0} \frac{ \frac{f(x+h)}{g(x+h)} - \frac{f(x)}{g(x)}}{h} = \\ & = \lim_{h \rightarrow 0} \frac{\frac{f(x+h) g(x) - f(x) g(x+h)}{g(x) g(x+h)}}{h} = \\ & = \lim_{h \rightarrow 0} \frac{f(x+h) g(x) - f(x) g(x) + f(x) g(x) - f(x) g(x+h)}{h g(x) g(x+h)} = \\ & = \dots \\ & = \frac{f'(x) g(x) - f(x) g'(x)}{g^2(x)} \ . \end{aligned}\end{split}\]
Dimostrazione della regola della funzione composta

La derivata in \(x\) della funzione \(f(g(x))\) viene calcolata con la definizione di limite di rapporto incrementale, a \(x\) costante per \(h \rightarrow 0\)

\[\begin{split}\begin{aligned} \left( f(g(x)) \right)' & = \lim_{h \rightarrow 0} \frac{ f(g(x+h)) - f(g(x)) }{h} = \\ & = \lim_{h \rightarrow 0} \frac{ f(g(x+h)) - f(g(x)) }{h} \frac{g(x+h) - g(x)}{g(x+h)-g(x)} = \\ & = \lim_{h \rightarrow 0} \frac{ f(g(x+h)) - f(g(x)) }{g(x+h) - g(x)} \frac{g(x+h)-g(x)}{h} = \\ & = \dots = \\ & = f'\left( g(x) \right) g'(x) \ . \end{aligned}\end{split}\]

  • todo discutere la validità dell’operazione di moltiplicare per \(\frac{g(x+h) - g(x)}{g(x+h) - g(x)}\)

  • todo \(g(x+h) - g(x)) \rightarrow 0\) per \(h \rightarrow 0\) poiché \(g(x)\) è continua se derivabile

Dimostrazione della regola della funzione inversa

Si usa la regola (24.8) di derivazione della funzione composta applicata alla relazione

\[x = f^{-1} \left( f(x) \right)\]

che caratterizza la funzione inversa \(f^{-1}\). Derivando entrambi i termini della relazione rispetto alla variabile indipendente \(x\) si ottiene

\[1 = \dfrac{d f^{-1}}{d y}\bigg|_{y = f(x)} \, \dfrac{d f(x)}{d x} \ ,\]

dalla quale segue immediatamente la regola di derivazione della funzione inversa

\[ \dfrac{d f^{-1}}{d y}\bigg|_{y = f(x)} = \dfrac{1}{ \dfrac{d y}{d x}\bigg|_{x}} \ .\]

24.5. Teoremi#

24.5.1. Teorema di Fermat#

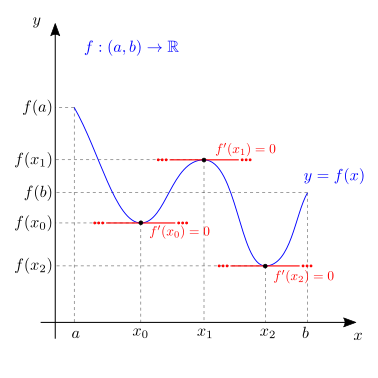
Theorem 24.1 (Teorema di Fermat)

Data la funzione \(f: (a,b) \rightarrow \mathbb{R}\) derivabile nel punto di estremo locale \(x_0 \in (a,b)\), allora \(f'(x_0) = 0\).
Dimostrazione

Sia \(x_0\) un punto di minimo locale della funzione \(f(x)\) derivabile in \(x_0\). La definizione di minimo locale permette di scrivere

\[\exists \delta > 0: \ x in (x_0 - \delta, x_0 + \delta) \cap (a,b) \quad \rightarrow \quad f(x_0) \le f(x) \ .\]

Quindi si possono scrivere le seguenti relazioni

\[\frac{f(x_0 + h) - f(x_0)}{h} \ge 0 \qquad \forall h \in (0, \delta)\]
\[\frac{f(x_0 + h) - f(x_0)}{h} \le 0 \qquad \forall h \in (-\delta,0)\]

Il limite per \(h \rightarrow 0\) di queste due relazioni esiste ed è \(f'(x_0)\) in entrambi i casi, essendo la derivata il limite del rapporto incrementale. Le due espressioni a sinistra dei segni di disuguaglianza possono essere considerate funzioni continue della variabile \(h\), il cui limite esiste per \(h \rightarrow 0\). Usando il teorema della permanenza del segno, si può concludere che

\[\begin{split}\begin{cases} f'(x_0) \ge 0 \\ f'(x_0) \le 0 \\ \end{cases}\end{split}\]

e da queste la dimostrazione della tesi del problema, \(f'(x_0)\).

24.5.2. Teorema di Rolle#

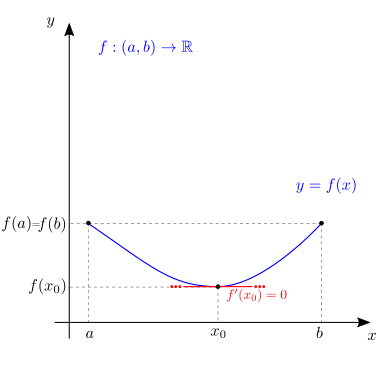
Theorem 24.2 (Teorema di Rolle)

Data la funzione \(f: [a,b] \rightarrow \mathbb{R}\) continua e derivabile in ogni punto dell’intervallo \((a,b)\) con \(f(a) = f(b)\), allora esiste un valore \(c \in (a,b)\) in cui \(f'(c) = 0\).

Dimostrazione

Per il teorema di Weierstrass, la funzione \(f\) ha un massimo \(M\) e un minimo \(m\) assoluti nell’intervallo \([a,b]\). Si distinguono due casi:

  • massimo e minimo sono nei punti estremi dell’intervallo. Allora la funzione è costante, e la derivata è nulla in ogni punto \(c \in (a,b)\)

  • i punti di massimo e di minimo sono interni all’intervallo. In questo caso, per il teorema di Fermat i punti \(c\) di minimo o massimo verificano la condizione \(f'(c) = 0\).

24.5.3. Teorema di Cauchy#

Theorem 24.3 (Teorema di Cauchy)

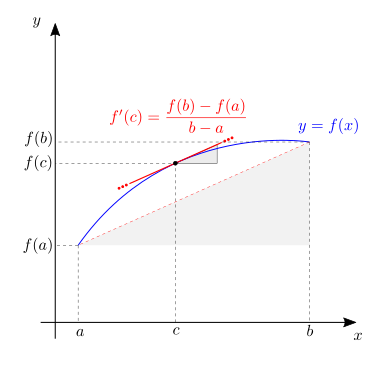
Date le funzioni \(f, g: [a,b] \rightarrow \mathbb{R}\) continue in \([a,b]\) e derivabili in \((a,b)\), allora esiste almeno un punto \(c \in (a,b)\) tale che

\[\left[ g(b) - g(a) \right] \, f'(c) = \left[ f(b) - f(a) \right] \, g'(c) \ .\]
Dimostrazione

Si applica il teorema di Rolle alla funzione

\[h(x) = \left[ g(b) - g(a) \right] \, f(x) - \left[ f(b) - f(a) \right] \, g(x)\]

continua in \([a,b]\), derivabile in \((a,b)\) e con \(h(a) = g(b) \, f(a) - f(b) \, g(a) = h(b)\).

24.5.4. Teorema di Lagrange#

Theorem 24.4 (Theorema di Lagrange)

Data la funzione \(f, g: [a,b] \rightarrow \mathbb{R}\) continua in \([a,b]\) e derivabile in \((a,b)\), allora esiste un valore \(c \in (a,b)\) tale che

\[f(b) - f(a) = (b - a) f'(c) \ .\]
Dimostrazione

Si applica il teorema di Cauhcy scegliendo la funzione \(g(x) = x\).

24.5.5. Teorema di de l’Hopital#

Theorem 24.5 (Teorema di de l’Hopital )

Siano \(f(x), g(x): [a,b] \rightarrow \mathbb{R}\) funzioni reali di variabile reale continue in \([a,b]\) e derivabili in \((a,b) \backslash \{ x_0 \}\).

\[\begin{aligned} & \lim_{x \rightarrow x_0} f(x) = \lim_{x \rightarrow x_0} g(x) = 0 \qquad \text{oppure} & \lim_{x \rightarrow x_0}|f(x)|= \lim_{x \rightarrow x_0}|g(x)|= \infty \end{aligned}\]

Se esiste

\[ \lim_{x \rightarrow x_0} \frac{f'(x)}{g'(x)} = \ell \quad \text{finito}\]

allora

\[ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = \ell \ . \]

todo Controllare l’enunciato

Dimostrazione

Forma indeterminata \(\frac{0}{0}\). Usando il teorema di Cauchy e il teorema di Rolle todo

Forma indeterminata \(\frac{\infty}{\infty}\). Usando il teorema di Cauchy e il teorema di Lagrange todo

Oss. Il teorema di de l’Hopital può essere applicato anche in successione, più di una volta, fermandosi al primo rapporto di derivate dello stesso ordine che non produce una forma indeterminata.

24.6. Derivate fondamentali#

Usando i limiti fondamentali, vengono calcolate le derivate fondamentali, che a loro volta permettono il calcolo degli integrali fondamentali. Le derivate fondamentali e la loro combinazione con le regole di derivazione permettono la derivazione di funzioni generiche. Le derivate fondamentali sono:

(24.10)#\[\begin{split}\begin{aligned} f(x) & = x^n \qquad & \qquad f'(x) & = n x^{n-1} \\ f(x) & = e^x \qquad & \qquad f'(x) & = e^x \\ f(x) & = \ln x \qquad & \qquad f'(x) & = \frac{1}{x} \\ f(x) & = \sin x \qquad & \qquad f'(x) & = \cos x \\ f(x) & = \cos x \qquad & \qquad f'(x) & =-\sin x \end{aligned}\end{split}\]
Dimostrazione di \(\ (x^n)'\)

Usando la formula binomiale \((x + \varepsilon)^n = x^n + n x^{n-1} \varepsilon + f(\varepsilon^2, \varepsilon^3, \dots)\),

\[\begin{split}\begin{aligned} \dfrac{d}{dx} x^n & = \lim_{\varepsilon \rightarrow 0} \dfrac{(x+\varepsilon)^{n} - x^n}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{x^n + n x^{n-1} \varepsilon + o(\varepsilon) - x^n}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \left( n x^{n-1} + O(\varepsilon) \right) = \\ & = n x^{n-1} \ . \end{aligned}\end{split}\]
Dimostrazione di \(\ (e^x)'\)

Usando le proprietà della funzione esponenziale e il limite \(e^{\varepsilon} - 1 \sim \varepsilon\) per \(\varepsilon \rightarrow 0\)

\[\begin{split}\begin{aligned} \dfrac{d}{dx} e^x & = \lim_{\varepsilon \rightarrow 0} \dfrac{e^{x+\varepsilon} - e^x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{e^x \left( e^{\varepsilon} - 1 \right)}{\varepsilon} = \\ & = e^x \lim_{\varepsilon \rightarrow 0} \dfrac{\varepsilon + o(\varepsilon)}{\varepsilon} = \\ & = e^x \lim_{\varepsilon \rightarrow 0} \left( 1 + O(\varepsilon) \right) = \\ & = e^x \ . \end{aligned}\end{split}\]
Dimostrazione di \(\ (\ln x)'\)

Usando le proprietà della funzione logaritmo naturale e il limite \(\ln(1 + \varepsilon) \sim \varepsilon\) per \(\varepsilon \rightarrow 0\), per \(x > 0\)

\[\begin{split}\begin{aligned} \dfrac{d}{dx} \ln x & = \lim_{\varepsilon \rightarrow 0} \dfrac{\ln(x+\varepsilon) - \ln x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\ln \left(1 + \frac{\varepsilon}{x} \right)}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\frac{\varepsilon}{x} + o(\varepsilon)}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \left( \frac{1}{x} + O(\varepsilon) \right) = \\ & = \frac{1}{x} \ . \end{aligned}\end{split}\]
Dimostrazione di \(\ (\sin x)'\)

Usando le formule di somma delle funzioni armoniche, todo ref, e gli infinitesimi delle funzioni \(\sin \varepsilon \sim \varepsilon\), \(\cos \varepsilon \sim 1 - \frac{\varepsilon^2}{2}\) per \(\varepsilon \rightarrow 0\),

\[\begin{split}\begin{aligned} \dfrac{d}{dx} \sin(x) & = \lim_{\varepsilon \rightarrow 0} \dfrac{\sin(x+\varepsilon) - \sin x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\sin x \cos \varepsilon + \cos x \sin \varepsilon - \sin x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\sin x \left( 1 - \frac{\varepsilon^2}{2} \right) + \varepsilon \, \cos x - \sin x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \left( \cos x + O(\varepsilon) \right) = \\ & = \cos x \ . \end{aligned}\end{split}\]
Dimostrazione di \(\ (\cos x)'\)

Usando le formule di somma delle funzioni armoniche, todo ref, e gli infinitesimi delle funzioni \(\sin \varepsilon \sim \varepsilon\), \(\cos \varepsilon \sim 1 - \frac{\varepsilon^2}{2}\) per \(\varepsilon \rightarrow 0\),

\[\begin{split}\begin{aligned} \dfrac{d}{dx} \cos(x) & = \lim_{\varepsilon \rightarrow 0} \dfrac{\cos(x+\varepsilon) - \cos x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\cos x \cos \varepsilon - \sin x \sin \varepsilon - \sin x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \dfrac{\cos x \left( 1 - \frac{\varepsilon^2}{2} \right) - \varepsilon \, \sin x - \cos x}{\varepsilon} = \\ & = \lim_{\varepsilon \rightarrow 0} \left( - \sin x + O(\varepsilon) \right) = \\ & = - \sin x \ . \end{aligned}\end{split}\]

24.7. Derivate di ordine superiore#

Nel calcolo delle derivate di ordine superiore non c’è nulla di speciale: una volta che si è in grado di calcolare la derivata di una funzione reale, la derivata di ordine \(n\) viene calcolata applicando \(n\) volte l’operatore derivata alla funzione.

24.8. Serie di Taylor e MacLaurin#

Le espansioni in serie di Taylor e di MacLaurin sono serie polinomiali che forniscono un”approssimazione locale di una funzione, valida nell’intorno (todo valutare questa espressione) di un punto.

La serie di Taylor della funzione \(f(x)\) in un intervallo centrato in \(x_0\) è la serie

\[\begin{split}\begin{aligned} T[f(x); x_0] & = \sum_{n=0}^{\infty} \dfrac{f^{(n)}(x_0)}{n!} (x-x_0)^n = \\ & = f(x_0) + f'(x_0) (x-x_0) + \dfrac{f''(x_0)^2}{2!} (x-x_0)^2 + \dots \ . \end{aligned}\end{split}\]

La serie di MacLaurin è la serie di Taylor centrata in \(x_0 = 0\). La serie di Taylor troncata al grado \(N\) è il polinomio di grado \(N\) formato dalla sommatoria dei primi \(N+1\) termini della serie di Taylor,

\[T_N[f(x); x_0] = \sum_{n=0}^{N} \dfrac{f^{(n)}(x_0)}{n!} (x-x_0)^n \ .\]

La serie di Taylor troncata al \(N\)-esimo termine fornisce un’approssimazione locale della funzione \(f(x)\) di ordine \(n\), nel senso definito dal seguente teorema.

Theorem 24.6 (Approssimazione locale)

todo Ipotesi del teorema.

Valgono i seguenti risultati di approssimazione locale

  • La serie di Taylor di ordine \(N\) è un’approssimazione locale di ordine \(N\) della funzione

    \[\lim_{x \rightarrow x_0} \frac{f(x) - T_N[f(x); x_0]}{(x-x_0)^N} = 0 \ , \]

    o usando la notazione di «o piccolo» per il confronto di infinitesimi,

    \[f(x) = T_N[f(x); x_0] + o\left((x-x_0)^N\right) \quad \text{ per } \quad x \rightarrow x_0 \ .\]

  • L’errore di approssimazione di ordine \(N+1\) è asintotico a

    \[f(x) - T_N[f(x); x_0] \sim \frac{f^{(N+1)}}{(N+1)!} (x - x_0)^{N+1} \quad x \rightarrow x_0 \ \]
Dimostrazione

Usando il teorema di de l’Hopital, fino a quando il rapporto non è una forma indeterminata

\[\begin{split}\begin{aligned} \lim_{x \rightarrow x_0} \frac{f(x) - T_N[f(x); x_0]}{(x-x_0)^N} & = \lim_{x \rightarrow x_0} \dfrac{f(x) - f(x_0) + f'(x_0) (x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \dots \frac{f^{(N)}(x_0)}{N!}(x-x_0)^N}{(x-x_0)^N} = \text{(H)} = \\ & = \lim_{x \rightarrow x_0} \dfrac{f'(x) - f'(x_0) + \frac{f''(x_0)}{1!} (x-x_0) + \dots \frac{f^{(N)}(x_0)}{(N-1)!}(x-x_0)^{N-1}}{N \, (x-x_0)^{N-1}} = \text{(H)} = \\ & = \lim_{x \rightarrow x_0} \dfrac{f''(x) - f''(x_0) + \dots \frac{f^{(N)}(x_0)}{(N-2)!}(x-x_0)^{N-2}}{N \, (N-1) \, (x-x_0)^{n-1}} = \text{(H)} =\\ & = \dots \\ & = \lim_{x \rightarrow x_0} \dfrac{f^{(N)}(x) - f^{(N)}(x_0)}{N!} = 0 \ , \end{aligned}\end{split}\]

si dimostra che il numeratore è un infinitesimo dello stesso ordine del denominatore. Usando la notazione dell”»o piccolo» per gli infinitesimi si può quindi scrivere l’approssimazione locale come:

\[f(x) - T_N[f(x), x_0] = o\left((x-x_0)^N\right) \ ,\]

o in maniera equivalente

\[f(x) = T_N[f(x), x_0] + o\left((x-x_0)^N\right) \ .\]

Ripetendo lo stesso procedimento, confrontando la differenza \(f(x) - T_N[f(x);x_0]\) con il termine \((x-x_0)^{N+1}\) si ottiene

\[ \lim_{x \rightarrow x_0} \frac{f(x) - T_N[f(x); x_0]}{(x-x_0)^N} = \dots = \lim_{x \rightarrow x_0} \frac{f^{(N+1)}(x)}{(N+1)!} = \frac{f^{(N+1)}(x_0)}{(N+1)!} \ . \]

24.8.1. Esempi#

La serie di MacLaurin per le funzioni interessate nei limiti notevoli forniscono approssimazioni locali di ordine maggiore per \(x \rightarrow 0\),

(24.11)#\[\begin{split}\begin{aligned} \cos(x) & = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + o(x^5) \\ \sin(x) & = x - \frac{x^3}{3!} + \frac{x^5}{5!} + o(x^6) \\ \ln (1+x) & = x - \frac{x^2}{2} + \frac{x^3}{3} + o(x^3) \\ (1+x)^a & = 1 + a x + a(a-1) \frac{x^2}{2} + o(x^2) \\ e^x & = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + o(x^5) \end{aligned}\end{split}\]

todo Dimostrare la convergenza delle serie. Convergenza puntuale, convergenza uniforme (in un insieme di convergenza, di solito centrato in un punto e le cui dimensioni sono definite da un raggio di convergenza)

Rivisitazione limiti notevoli Per \(x \rightarrow 0\)

\[\begin{split}\begin{aligned} \sin x & = x +o(x) \\ 1 - \cos x & = \frac{1}{2} x^2 + o(x^3) \\ e^x - 1 & = x + o(x) \\ \ln(1+x) & = x + o(x) \\ (1+x)^a - 1 & = a \, x + o(x) \\ \end{aligned}\end{split}\]

Identità di Eulero. Usando l’espansione in serie di Taylor per l’esponenziale complesso \(e^{ix}\), si ottiene

\[\begin{split}\begin{aligned} e^{ix} & = 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{x^5}{5!} + o(x^5) = \\ & = \Big( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} \Big) + i \Big( x - \frac{x^3}{3!} + \frac{x^5}{5!} \Big) + o(x^5) = \\ & = \cos x + i \sin x \ . \end{aligned}\end{split}\]

24.9. Applicazioni#

24.9.1. Approssimazioni locali#

Le serie di Taylor e di MacLaurin e le proprietà di approssimazione riassunte nel Theorem 24.6 permettono di ricavare un’approssimazione locale di una funzione \(f(x)\) nella forma di serie polinomiali.

…

24.9.2. Studio di funzione#

Uno studio di funzione completo può richiedere la padronanza di tutti gli strumenti del calcolo infinitesimale: ricerca del dominio, limiti, derivate e integrali.

24.9.3. Ottimizzazione#

24.9.4. Metodo di Netwon per la soluzione di equazioni algebriche \(f(x) = 0\)#

Due algoritmi iterativi classici usati per la soluzione di equazioni algebriche della forma \(f(x) = 0\) - problema che può essere descritto come ricerca degli zeri della funzione \(f(x)\) - sono il metodo di bisezione e il metodo di Newton. Il metodo di bisezione viene discusso nella sezione sull’introduzione all’analisi, mentre qui viene presentato il meetodo di Newton.

…

Il metodo di Newton è discusso nel bbook sull’introduzione alla programmazione e al calcolo scientifico, nella sezione di introduzione al calcolo numerico. Nella sezione sui metodi numerici per la soluzione di equazioni algebriche non lineari, il metodo di Newton viene descritto, implementato e applicato a semplici esempi.