13.4. Rette nello spazio#
13.4.1. Definizione ed equazione#
Definizione 1 - Passaggio per un punto e direzione tangente. I punti \(P\) della retta \(r\) passante per il punto \(P_0\) e con direzione \(\vec{v}\) possono essere rappresentati dall”equazione parametrica,
Questa relazione può essere scritta usando un sistema di coordidnate carteisane, con base \(\{ \hat{x}, \hat{y}, \hat{z} \}\),
Definizione 2 - Interesezione di due piani incidenti. todo
13.4.2. Posizioni reciproche#
13.4.2.1. Posizione reciproca di punto e retta#
Un punto \(P\) o appartiene o non appartiene a una retta \(r\).
13.4.2.1.1. Distanza punto-retta#
Dato un punto \(A\) e una retta \(r\), di cui sono noti un punto \(Q\) e il vettore \(\vec{v}\), la distanza di \(A\) da \(r\) può essere calcolata come il valore assoluto della proiezione del vettore \(A-Q\) in direzione ortogonale alla direzione della retta, individuata da \(\vec{v}\),
avendo usato il vettore unitario \(\hat{v} = \frac{\vec{v}}{|\vec{v}|}\) per la proiezione.
13.4.2.2. Posizione reciproca retta e piano#
Una retta \(r\) può essere:
contenuta in un piano \(\pi\): ha tutti i punti appartenenti al piano
parallela a un piano \(\pi\): non ha nessun punto appartenente al piano
incidente a un piano \(\pi\): interseca il piano in un solo punto
13.4.2.3. Posizione reciproca tra rette#
Due rette possono essere:
coincidenti: hanno tutti i punti in comune
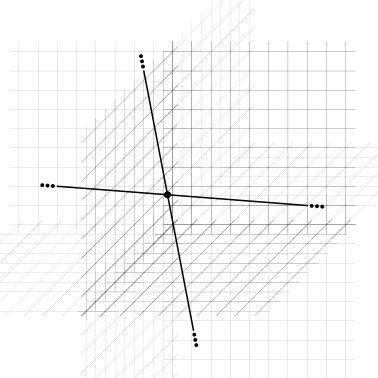
incidenti: si intersecano in un solo punto
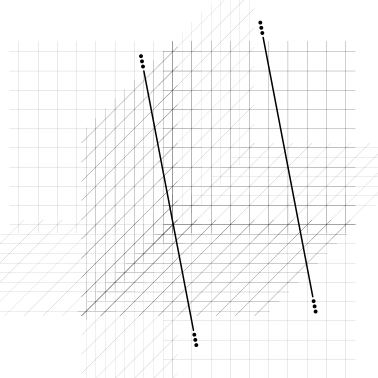
parallele: non hanno nessun punto in comune e hanno la stessa direzione; esiste un piano che contiene entrambe le rette
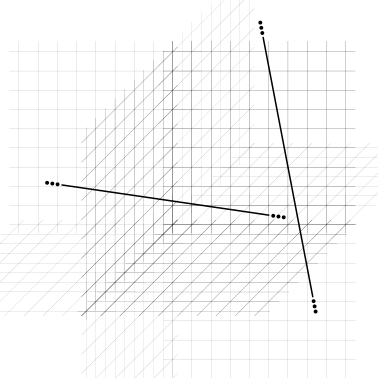
sghembe: non hanno nessun punto in comune e hanno direzioni diverse; non esiste nessun piano che contiene entrambe le rette
todo verificare queste condizioni
|
|
|