13.1. Sistemi di coordinate per lo spazio euclideo \(E^3\)

13.1.1. Coordinate cartesiane

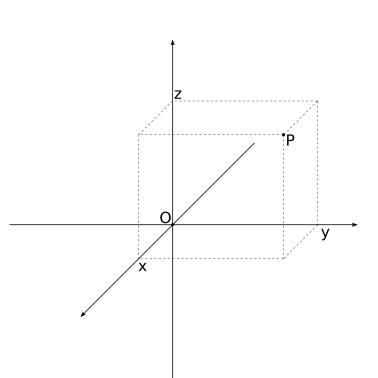
Le coordinate cartesiane \((x,y,z)\) di un punto \(P\) dello spazio euclideo \(E^3\) permettono di definire il vettore euclideo tra l’origine \(O \equiv (0,0,0)\) e il punto \(P\)

\[(P-O) = x \, \hat{x} + y \, \hat{y} + z \, \hat{z} \ ,\]

usando i vettori della base cartesiana \(\{ \hat{x}, \hat{y}, \hat{z} \}\)

13.1.1.1. Distanza punto-punto

Usando le coordinate cartesiane, la distanza tra due punti \(P \equiv(x_P, y_P, z_P)\), \(Q \equiv (x_Q, y_Q, z_Q)\) si può calcolare usando il teorema di Pitagora come

\[|P-Q|^2 = (x_P - x_Q)^2 + (y_P - y_Q)^2 + (z_P - z_Q)^2 \ .\]

13.1.2. Coordinate cilindriche

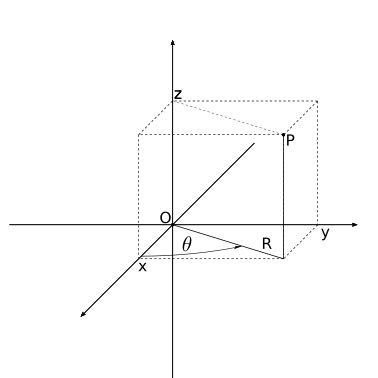
Dato un sistema di coordinate cartesiane, si può definire un sistema di coordinate cilindriche \((R, \theta, z)\) con la stessa origine, asse \(z\) coincidente e usando il piano \(x\)-\(y\) come origine per misurare l’angolo \(\theta\) attorno all’asse \(z\), tramite la legge di trasformazione delle coordinate

\[\begin{split}\begin{cases} x = R \cos \theta \\ y = R \sin \theta \\ z = z \end{cases}\end{split}\]

13.1.3. Coordinate sferiche

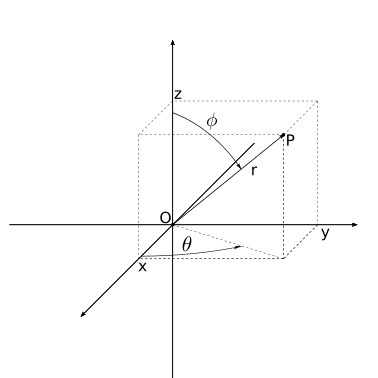
Dato un sistema cartesiano e scelto un sistema di coordinate cilindriche come appena descritto, si può definire un sistema di coordinate sferiche \((r, \theta, \phi)\) tramite le leggi di trasformazione di coordinate

\[\begin{split} \begin{cases} x = r \sin \phi \, \cos \theta \\ y = r \sin \phi \, \sin \theta \\ z = r \cos \phi \end{cases} \qquad , \qquad \begin{cases} R = r \sin \phi \\ \theta = \theta \\ z = r \cos \phi \\ \end{cases} \end{split}\]