18.2.4.2. Moneta truccata#
Si vuole valutare se una moneta è truccata. L’ipotesi nulla \(\text{H}_0\) da falsificare è «la moneta non è truccata». Si sceglie come statistica test la percentuale di risultati «testa» sul numero di lanci.
L’esperimento viene condotto per un numero incrementale di esperimenti.
18.2.4.2.1. Import librerie e funzioni utili#
18.2.4.2.1.1. Import librerie#
Reset delle variabili e import librerie.
Show code cell source
%reset -f
# Import libraries
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
18.2.4.2.2. Funzione per lo svolgimento di un esperimento#
La funzione per lo svolgimento di un esperimento qui definita prende come argomenti un generatore di numeri casuali e i suoi parametri, e restituisce i campioni prodotti secondo la distribuzione data. Vengono definiti dei parametri di default, corrispondenti a una distribuzione di Bernoulli uniforme
Show code cell source
#> Random process of interest, unknown execpt for the sample.
p_head_default = .5
p_tail_default = 1. - p_head_default
# Coin flip as a Bernoulli probability with outcomes: a = [0, 1] with prob p = [p_head, p_tail]
flip_rng_default = np.random.default_rng(42).choice
flip_params_default = { 'a': [0,1], 'p': [p_head_default, p_tail_default], 'size': 1 } # default params
def run_experiment(rng=flip_rng_default, rng_params=flip_params_default):
return rng(**rng_params)
18.2.4.2.2.1. Funzione che restituisce la pdf \(p(x|\text{H}_0)\)#
Show code cell source
# ! Approach for low-dimensional problems, with no memory or performance issues
#> Null hypotesis, H0: the coin is fair
# # The outcome of a single flip is a r.v. distributed like a Bernoulli variable with p_head = .5
# # Every flip is statistically independent from the other
# ixv= np.arange(n_flips+1)
# xv = ixv / n_flips
#
# #> Test statistics: average n.of heads in flip_n samples
# # H0 hypotesis implies that the outcome of flip_n is a r.v. with Binomial pdf
# x_H0_fv = sp.stats.binom.pmf(ixv, n_flips, p_head)
def px_H0(p, p_params,):
return p(**p_params)
18.2.4.2.2.2. Funzioni per la ricerca degli intervalli di accettazione dell’ipotesi#
Vengono qui definite due funzoni per la ricerca degli intervalli di accettazione, dato il livello di significatività del test richiesto. La prima funzione ricerca un unico intervallo di accettazione riferito a un unico livello di significatività; la seconda funzione ricerca tanti intervalli di accettazione quanti sono i livelli di significatività cercati: ad esempio, si possono cercare simultaneamente i livellidi significatività associati a \(\sigma\), \(2 \sigma\), \(3 \sigma\)…
Show code cell source
#> Acceptance and rejection regions, for discrete pdf
# Starting from the value of the test statistics x_max = max(x_H0_fv), expand
def find_acceptance_region(p, alpha, test_type='value'):
"""
Find acceptance region for a discrete pdf, supposed to be unimodal
for a given value of significance level
test_type is not used so far...
"""
x_max = np.argmax(p)
nx = len(p)
threshold = 1. - alpha
# Initialization
p_acc, xl, xr = p[x_max], x_max, x_max
# if ( test_type == 'value' ):
while ( p_acc < threshold ):
if ( p[xl-1] >= p[xr+1] ):
xl -= 1; p_acc += p[xl]
else:
xr += 1; p_acc += p[xr]
# else:
return xl, xr
def find_acceptance_regions(p, alpha_v, test_type='value'):
"""
Find acceptance region for a discrete pdf, supposed to be unimodal
for a set of values of significance levels, type(alpha_v) = numpy.array
test_type is not used so far...
"""
#> Dimensions
ix_max = np.argmax(p)
nx, nal = len(p), len(alpha_v)
ixlv, ixrv = np.zeros(nal), np.zeros(nal)
#> Sorting
alpha_v = np.sort(alpha_v)[::-1]
threshold_v = 1. - alpha_v
# Initialization
p_acc, ixl, ixr = p[ix_max], ix_max, ix_max
#> Loop over all the thresholds
for ial in np.arange(nal):
while ( p_acc < threshold_v[ial] ):
if ( p[ixl-1] > p[ixr+1] ):
ixl -= 1; p_acc += p[ixl]
else:
ixr += 1; p_acc += p[ixr]
ixlv[ial], ixrv[ial] = ixl, ixr
return ixlv, ixrv
#> Test
# n_flips = 160
# x_H0_fv = sp.stats.binom.pmf(np.arange(n_flips+1), n_flips, .5) # p_fair_coin .5
# xlv, xrv = find_acceptance_regions(x_H0_fv, alpha_v,)
# print(xlv, xrv)
18.2.4.2.3. Esperimento#
18.2.4.2.3.1. Livelli di accettazione#
Show code cell source
#> Test characteristics: symmetric
test_type = 'value' # 'symmetric', 'right', 'left', 'value'
#> Significance level, alpha = .05 ("default")
alpha = .05
alpha_v = np.array([ .3, .05, .003 ])
18.2.4.2.3.2. Svolgimento esperimento#
L’esperimento viene svolto usando due monete, la cui natura è a priori incognita, che possono essere modellate con variabili casuali di Bernoulli: una moneta non truccata produce testa o croce con la probaiblità uniforme \(0.5\); una moneta truccata che produce testa o croce con probabilità \(0.45 - 0.55\)
Show code cell source
#> Run experiments, with incremental number of samples
n_flips_1 = 20
n_flips_max = 5000
n_flips = 0
H0_true = True
ov_fair, ov_rigg = [], []
xlv, xrv, xsv_fair, xsv_rigg, n_flipsv = [], [], [], [], []
flip_rng = np.random.default_rng().choice
flip_params_fair = { 'a': [0,1], 'p': [.5 , .5 ], 'size': n_flips_1 } # default params
flip_params_rigg = { 'a': [0,1], 'p': [.45, .55], 'size': n_flips_1 } # default params
while ( n_flips < n_flips_max and H0_true ):
#> Run a new experiment and collect new n_flips_1 samples
n_flips += n_flips_1
ov_fair_1 = run_experiment(rng=flip_rng, rng_params=flip_params_fair)
ov_rigg_1 = run_experiment(rng=flip_rng, rng_params=flip_params_rigg)
ov_fair += list(ov_fair_1)
ov_rigg += list(ov_rigg_1)
#> Find distribution function
x_H0_fv = px_H0(sp.stats.binom.pmf, {'k': np.arange(0,n_flips+1), 'n': n_flips, 'p': .5}) # H0: fair coin
#> Evaluate acceptance region
ixl, ixr = find_acceptance_regions(x_H0_fv, alpha_v,)
# print(n_flips, ixl, ixr)
#> Evaluate test statistics on the sample
ixs_fair = np.sum(ov_fair)
ixs_rigg = np.sum(ov_rigg)
#> Check if H0 is not false. If commented, let the while run until n_flips = n_flips_max
# if ( ixl[-1] > ix_s or ixr[-1] < ix_s ):
# H0_true = False
#> Store quantities for plots
n_flipsv += [ n_flips ]
xlv += [ ixl/n_flips ]
xrv += [ ixr/n_flips ]
xsv_fair += [ ixs_fair/n_flips ]
xsv_rigg += [ ixs_rigg/n_flips ]
/home/davide/.local/lib/python3.8/site-packages/scipy/stats/_discrete_distns.py:77: RuntimeWarning: divide by zero encountered in _binom_pdf
return _boost._binom_pdf(x, n, p)
18.2.4.2.3.3. Grafici#
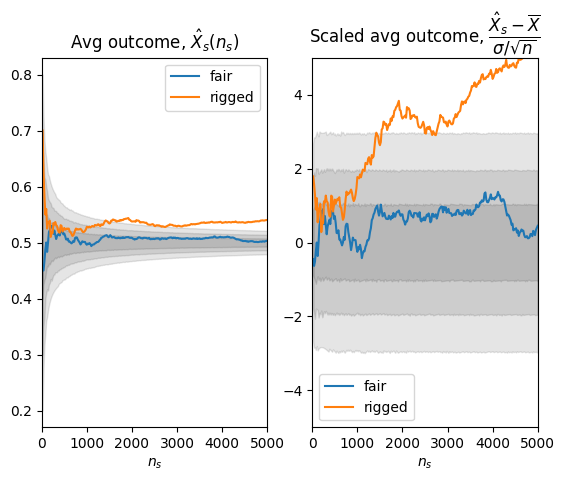
Il valore medio delle volte che è uscita croce viene usata come statistica test. Il valore della statistica test per gli esperimenti condotti con le due monete viene confrontato con la funzione di distribuzione \(p(x|\text{H}_0)\) per una moneta non truccata. Viene mostrato l’andamento delle statistiche test e degli intervalli di accettazione in funzione del numero di lanci della moneta. Vengono mostrati i dati raccolti e successivamente depurati della media attesa e scalati per la varianza della media campionaria \(\frac{\sigma}{\sqrt{n_s}}\), per mettere in evidenza i livelli di significatività \([0.3, 0.05, 0.003]\)
Show code cell source
#> Convert list to numpy arrays, to perform some algebra below
n_flipsv = np.array(n_flipsv)
xlv = np.array(xlv)
xrv = np.array(xrv)
xsv_fair = np.array(xsv_fair)
xsv_rigg = np.array(xsv_rigg)
#>
plt.figure()
plt.subplot(1,2,1)
for ial in np.arange(len(alpha_v)):
# plt.plot(n_flipsv, xlv[:,ial], color=plt.cm.tab10(ial))
# plt.plot(n_flipsv, xrv[:,ial], color=plt.cm.tab10(ial))
plt.fill_between(n_flipsv,
xlv[:,ial],
xrv[:,ial], color=(0,0,0,.1))
plt.plot(n_flipsv, xsv_fair, color=plt.cm.tab10(0), label='fair')
plt.plot(n_flipsv, xsv_rigg, color=plt.cm.tab10(1), label='rigged')
plt.xlim(0, n_flips)
#plt.ylim(-5, 5)
plt.title("Avg outcome, $\hat{X}_s(n_s)$")
plt.xlabel('$n_s$')
plt.legend()
#> For scaling results
bernoulli_avg, bernoulli_var = .5, .25
plt.subplot(1,2,2)
for ial in np.arange(len(alpha_v)):
# plt.plot(n_flipsv, xlv[:,ial], color=plt.cm.tab10(ial))
# plt.plot(n_flipsv, xrv[:,ial], color=plt.cm.tab10(ial))
plt.fill_between(n_flipsv,
(xlv[:,ial]-bernoulli_avg) * n_flipsv**.5/bernoulli_var**.5,
(xrv[:,ial]-bernoulli_avg) * n_flipsv**.5/bernoulli_var**.5, color=(0,0,0,.1))
plt.plot(n_flipsv, (xsv_fair-bernoulli_avg) * n_flipsv**.5/bernoulli_var**.5, color=plt.cm.tab10(0), label='fair')
plt.plot(n_flipsv, (xsv_rigg-bernoulli_avg) * n_flipsv**.5/bernoulli_var**.5, color=plt.cm.tab10(1), label='rigged')
plt.xlim(0, n_flips)
plt.ylim(-5, 5)
plt.title("Scaled avg outcome, $\dfrac{\hat{X}_s - \overline{X}}{\sigma/\sqrt{n}}$")
plt.xlabel('$n_s$')
plt.legend()
<matplotlib.legend.Legend at 0x7f8010228370>