18.2.1. Test su campioni singoli o coppie di campioni#
Test più comuni
\(t\)-test
\(\chi^2\)-test
\(Z\)-test
Wilcoxon
…
18.2.1.1. Student \(t\)-test#
I \(t\)-test sono dei test statistici di posizione in cui la statistica test segue una distribuzione \(t\) di Student sotto l’ipotesi nulla \(\text{H}_0\),
dove il numero di gradi di libertà \(\nu\) della distribuzione \(t_{\nu}\) dipende dal metodo considerato.
Questi test sono «esatti» se la popolazione ha distribuzione normale. todo in caso contrario, la statistica test costruita non segue una distribuzione \(t\)-Student. Bisogna valutare l’attendibilità del test in questo caso; per distribuzioni «sufficientemente simili a quella gaussiana» potrebbero essere validi; il teorema del limite centrale aiuta l’ipotesi di gaussianità; in caso di distribuzioni generiche, meglio affidarsi ad altri test - non parametrici
18.2.1.1.1. Test per un campione - valore medio#
E” un test di posizione/stima della media della popolazione della quale è noto un campione di \(N\) osservazioni, \(\mathbf{X} = \{ X_n \}_{n=1:N}\).
l’ipotesi nulla \(\text{H}_0\) dichiara che la popolazione ha media \(\mu_0\);
la statistica test \(T\),
\[T = \frac{\bar{X} - \mu_0}{\frac{S}{\sqrt{N}}} \ \]è costruita con la media e la varianza campionaria,
\[\bar{X} = \frac{1}{N} \sum_{n=1}^N X_n \qquad , \qquad S^2 = \frac{1}{N-1} \sum_{n=1}^N (X_n - \bar{X})^2 \ .\]
quindi, una volta definito il livello di significatività del test, \(\alpha\), si controlla se la statistica test \(t\) valutata con il campione a disposizione cade nella regione di rifiuto dell’ipotesi della distribuzione \(t_{N-1}\) o meno, per determinare se si deve considerare \(\text{H}_0\) falsificata dal test o meno
Ipotesi. Come dimostrato in appendice, se i campioni sono variabili i.i.d. gaussiane, con media \(\mu_0\) sotto l’ipotesi nulla \(\text{H}_0\), \(X_n \sim \mathscr{N}(\mu_0, \sigma^2)\), allora la statistica test segue una distribuzione \(t\)-Student con \(N-1\) gradi di libertà,
todo cosa succede quando la popolazione non ha distribuzione gaussiana? Qual è la robustezza del medoto alla caduta di questa ipotesi? Esempio già disponibile con campionamento variabile con distribuzione uniforme; altri metodi, non parametric?
18.2.1.1.2. Test per una coppia di campioni con stessa varianza - valore medio#
Un \(t\)-test per una coppia di campioni \(\{ X_{1,n} \}_{n=1:N}\), \(\{ X_{2,n} \}_{n=1:N}\) presi da due popolazioni \(X_1\), \(X_2\) di cui si ipotizza la stessa varianza \(\sigma^2\), si riduce al \(t\)-test per campione singolo per la variabile casuale \(X_2 - X_1\).
Variabili gaussiane. Nel caso in cui le variabili casuali \(X_1\), \(X_2\) abbiano distribuzione gaussiana con la stessa varianza, \(X_1 \sim \mathscr{N}(\mu_1, \sigma^2)\), \(X_2 \sim \mathscr{N}(\mu_2, \sigma^2)\), la variabile \(X_2 - X_1\) è gaussiana con distribuzione –>
todo
18.2.1.1.3. Altri \(t\)-test#
todo Se campioni di dimensione differente o con varianze differenti, Welct \(t\)-test…
18.2.1.2. \(Z\)-test#
Test identico al \(t\)-test in cui la statistica test \(z\) segue una distribuzione gaussiana sotto l’ipotesi nulla. Per il legame esistente tra la distribuzione \(t_{\nu}\) e \(\mathscr{N}\), si può interpretare lo \(Z\)-test come limite del \(t\)-test per un numero di campioni sufficientemente grande.
18.2.1.3. \(\chi^2\)-test di Pearson#
Il test \(\chi^2\) di Pearson si applica a dati categoriali, per confrontare le frequenze delle \(K\) categorie per diversi insiemi. Può essere applicato:
a un singolo campione, confrontando le frequenze osservate \(\{ O_k \}_{k=1:K}\) con le frequenze attese \(\{ E_k \}_{k=1:K}\), che costituiscono l’ipotesi nulla \(\text{H}_0\)
a più campioni (todo link a test di indipendenza statistica) per stabilire se provengono dalla stessa popolazione, o comunque da popolazioni con la stessa funzione di probabilità.
Il test \(\chi^2\) a un campione viene utilizzato per confrontare le frequenze osservate \(\{ O_k \}_{k=1:K}\) e attese \(\{ E_k \}_{k=1:K}\) di un insieme di possibili eventi, \(\{ X_n \}_{n=1:N}\).
l”ipotesi nulla \(\text{H}_0\) afferma che il fenomeno osservato segue la distribuzione di probabilità descritta dalle frequenze attese, \(\{ E_k \}\). Supponendo che i dati campionati siano iid, l’ipotesi nulla afferma che il fenomeno dal quale è estratto il campione segue una distribuzione di probabilità categoriale, \(\text{Categorial}(E_1,\dots,E_K)\)
La statistica test è
\[X^2 := \sum_{k=1}^{K} \frac{(O_k - E_k)^2}{E_k} \ ,\]
Nel caso in cui le frequenze attese sono «sufficientemente grandi» e quelle osservate \(O_k\) abbiano una distribuzione gaussiana, allora \(X^2\) segue una distribuzione \(\chi^2_{K-1}\).
… todo
18.2.1.3.1. Esempio: dado truccato#
Ci vengono dati due dadi a 6 facce e ci viene chiesto di verificare con \(n_{rolls} = 50\) lanci se questi dadi possono essere considerati truccati. Noi non lo sappiamo, ma il primo dado non è truccato, mentre il secondo dado è sbilanciato in modo tale che la possibilità che esca la faccia 3 è doppia rispetto a tutte le altre,
Show code cell source
# Reset env vars and load libraries
%reset -f
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
Show code cell source
# Random number generators representing dice roll
rng = np.random.default_rng(12345) # (12345) # initialize numpy default rng
# N.roll of the experiments
nrolls = 1000
# Categories: six-face dice X = [ 1,2,3,4,5,6 ]
categ = np.array([1,2,3,4,5,6])
n_categ = len(categ)
# Categorial probabilities of two dice, one fair, one not ( p_rigg(face3) = 2 p_rigg(facek) )
p_fair = np.array([1,1, 1, 1,1,1]) / 6. # fair dice
p_rigg = np.array([1,1, 2, 1,1,1]); p_rigg = p_rigg/np.sum(p_rigg) # rigged dice
# ...you can change p_ above, or add here other p_...
name_l = [ 'Fair', 'Rigged' ] # name of the experiments
prob_l = [ p_fair, p_rigg ] # collect data of experiments in a list
n_exp = len(prob_l) # n. of experiments
Ipotesi nulla. Per ogni esperimento, l’ipotesi nulla \(\text{H}_0\) è che il dado non sia truccato e che ogni faccia abbia una probabilità \(\frac{1}{6}\). La distribuzione di probabilità attesa è
Statistica test. Assumendo che la differenza tra le frequenze osservate e quelle attese abbiano una distribuzione gaussiana \(\sim \mathscr{N}(0, E^2)\), la statistica test ha una distribuzione
todo link al motivo per cui i dof sono \(N-1\): sostanzialmente poiché la pdf è determinata da un solo parametro, un solo vincolo, che riduce di 1 il numero di dof
Livello di significatività. Si sceglie un livello di significatività \(\alpha = 0.05\), cioè solo il \(5\%\) di casi estremi invalidano l’ipotesi nulla. Il livello di significatività determina il valore della statistica test che separa le regioni di accettazione e di rifiuto dell’ipotesi.
Show code cell source
# Null hypothesis, H0
# e_freq = nrolls * p_fair
# statistics ~ Chi^2_{n_categ - 1}
n_dofs = n_categ - 1 # n.dofs = n.categories - 1
# Significance level
alpha = .05 # .05, .01
# Point X2_rej_lim, discerning acceptance (X2 < X2_rej_lim) from rejection regions (X2 > X2_rej_lim)
X2_rej_lim = chi2.ppf(1-alpha, n_dofs)
Se si vuole essere più conservativi e rigettare l’ipotesi nulla «solo per dadi palesemente truccati», si può ridurre il livello di significatività del test. Ad esempio, scegliendo \(\alpha = 0.01\) si identificano come truccati solo i risultati estremi che hanno probabilità cumulata di verificarsi dell”\(1\%\) sotto l’ipotesi nulla (1% di falsi positivi).
Show code cell source
# Show influence of alpha on rejection set
print(f"\nRejection and acceptance regions for significance, alpha = {alpha}")
print(f"- Not rejection for X2 < {X2_rej_lim:.4f}")
print(f"- Rejection for X2 > {X2_rej_lim:.4f}")
print("\nRejection limits as a function of significance level")
alpha_l = [ .05, .01, .002, .0004 ]
for al in alpha_l:
print(f"X_rej_lim( alpha={al:0.3f} ) = {chi2.ppf(1-al, n_dofs):.4f}")
# Plot probability density, f(x), cumulative probability, F(x), and significance alpha(x)=1-F(x)
x_plot = np.arange(0., 25., .05)
fig, axes = plt.subplots(3, 1, figsize=(5,5))
axes[0].plot(x_plot, chi2.pdf(x_plot, n_dofs) )
axes[0].set_xlim([x_plot[0], x_plot[-1]])
axes[0].set_title(f"$\chi^2_{n_dofs}$")
axes[0].set_ylabel(f"pdf")
axes[0].grid()
axes[1].plot(x_plot, chi2.cdf(x_plot, n_dofs) )
axes[1].set_xlim([x_plot[0], x_plot[-1]])
axes[1].set_ylabel(f"cdf")
axes[1].grid()
axes[2].semilogy(x_plot, 1-chi2.cdf(x_plot, n_dofs) )
axes[2].set_xlim([x_plot[0], x_plot[-1]]); axes[2].set_xlabel('x')
# axes[2].fill_between(x_plot, 1-chi2.cdf(x_plot, n_dofs))
axes[2].set_ylabel(f"$\\alpha$")
for al in alpha_l:
xl = chi2.ppf(1-al, n_dofs)
axes[2].plot([0., xl, xl], [al, al, 1e-4], '--', color='red')
axes[2].grid()
Rejection and acceptance regions for significance, alpha = 0.05
- Not rejection for X2 < 11.0705
- Rejection for X2 > 11.0705
Rejection limits as a function of significance level
X_rej_lim( alpha=0.050 ) = 11.0705
X_rej_lim( alpha=0.010 ) = 15.0863
X_rej_lim( alpha=0.002 ) = 18.9074
X_rej_lim( alpha=0.000 ) = 22.6141
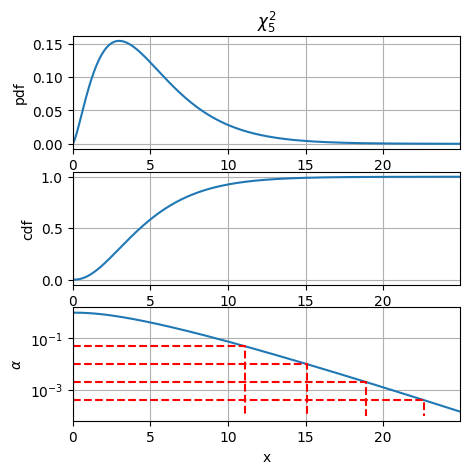
Vengono svolti gli esperimenti, raccolti i dati, calcolata la statistica test sui campioni e questa viene utilizzata per trarre le conclusioni sull’ipotesi nulla.
Show code cell source
# Function for running experiments
def run_experiments(categ, prob_l, nrolls):
# Expected frequencies
e_freq = nrolls * p_fair
# Initialize lists to collect data
o_freq_l = np.zeros((n_exp, 6),)
X2_v = np.zeros(n_exp, dtype=float)
# Loop over experiments
for i in range(n_exp):
# Roll the dice and collect outcomes
outcomes = rng.choice(categ, p=prob_l[i], size=nrolls)
# Count frequency of each category
unique_cat, counts = np.unique(outcomes, return_counts=True)
o_freq = np.zeros(6)
o_freq[unique_cat-1] = counts
# Store results
o_freq_l[i, :] = o_freq
X2_v[i] = np.sum((o_freq - e_freq)**2 / e_freq) # chi-2 statistics test (element-wise operations and sum)
return o_freq_l, X2_v
Show code cell source
# Run experiment
o_freq_l, X2_v = run_experiments(categ, prob_l, nrolls)
Show code cell source
fig, axes = plt.subplots(1, 2, figsize=(10,5))
for i in range(n_exp):
axes[i].bar(categ, o_freq_l[i,:])
axes[i].plot([0,7], 2*[nrolls/6], '--', color='red', label='Expected')
axes[i].set_xlim([.5,6.5])
axes[i].set_ylim([.0, nrolls/2])
axes[i].set_xlabel("Face")
axes[i].set_ylabel("Frequencies")
axes[i].grid(); axes[i].set_axisbelow(True)
axes[i].set_title(f"Experiment: {name_l[i]}, $X^2 = {X2_v[i]:.3f}$")
axes[i].legend()
plt.tight_layout()
plt.show()
Show code cell source
# Results
for i in range(n_exp):
print(f"Experiment: {name_l[i]}, nrolls: {nrolls}")
print(f"- probability (unknown in real exp.) : {np.array2string(prob_l[i], precision=4)}")
print(f"- Observed events : {np.array2string(o_freq_l[i], precision=4, )}")
print(f"- Test statistics, X2 : {X2_v[i]:.4f}")
if ( X2_v[i] < X2_rej_lim ):
print(f">> H0 not rejected ({X2_v[i]:.4f} < X_lim={X2_rej_lim:.4f}): dice is fair\n")
else:
print(f">> H0 rejected ({X2_v[i]:.4f} > X_lim={X2_rej_lim:.4f}): dice is rigged\n")
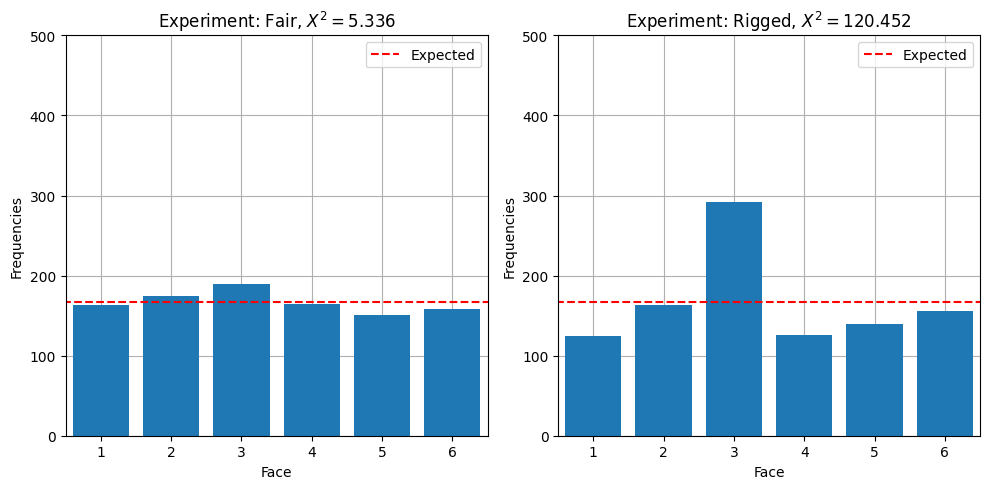
Experiment: Fair, nrolls: 1000
- probability (unknown in real exp.) : [0.1667 0.1667 0.1667 0.1667 0.1667 0.1667]
- Observed events : [163. 174. 189. 165. 151. 158.]
- Test statistics, X2 : 5.3360
>> H0 not rejected (5.3360 < X_lim=11.0705): dice is fair
Experiment: Rigged, nrolls: 1000
- probability (unknown in real exp.) : [0.1429 0.1429 0.2857 0.1429 0.1429 0.1429]
- Observed events : [124. 163. 292. 126. 139. 156.]
- Test statistics, X2 : 120.4520
>> H0 rejected (120.4520 > X_lim=11.0705): dice is rigged
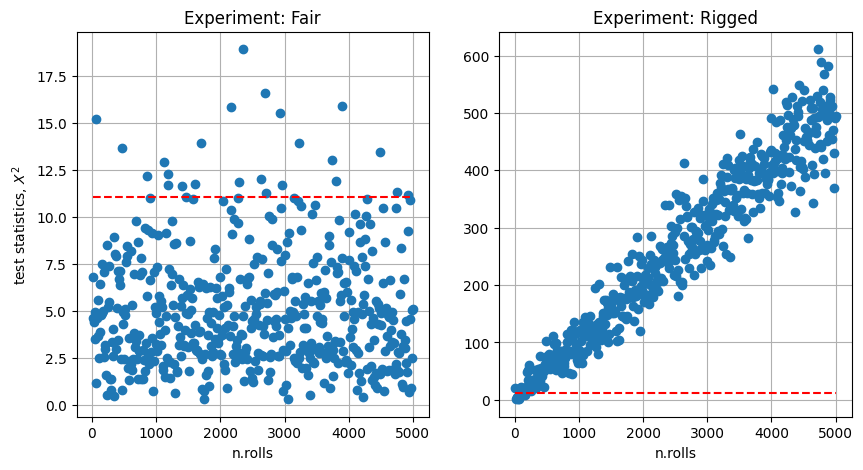
Dipendenza del risultato del test dal numero di prove. Si analizzano i risultati in funzione del numero di lanci fatti in ogni test. Si osserva che:
nel caso di dado non truccato la statistica test \(X^2\) non dimostra una convergenza (almeno fino a \(n_{rolls} = 5000\)) ma rimane limitata
nel caso di dado truccato, la statistica test \(X^2\) cresce circa linearmnete con il numero di lanci \(n_{rolls}\)
Nei \(500\) test svolti, il test ha dato risultati falso positivi nel \(4.8\%\) dei casi con \(\alpha = 0.05\) nel caso di dado non truccato (! ottimo, poiché il test si proponeva di rigettare proprio il \(5\%\) dei casi estremi), mentre ha riconosciuto il dado truccato come tale quasi tutte le volte.
Il progetto di un esperimento prevede la determinazione del numero di lanci necessario (senza andare troppo oltre! Tempo, soldi e pazienza sono una risorse finite!) per distinguere con la sufficiente accuratezza un dado truccato.
Show code cell source
# Run several tests with increasing number of rolls
nrolls_v = np.arange(10, 5001, 10)
ntests = len(nrolls_v)
# Initialize arrays to store test statistics value and count n.of rejections
X2_m = np.zeros((len(nrolls_v), n_exp), dtype=float)
rej_count = np.zeros(2,)
# Run experiments and collect results
for iroll in range(ntests):
freq, X2_m[iroll,:] = run_experiments(categ, prob_l, nrolls_v[iroll])
rej_count += (X2_m[iroll,:]>X2_rej_lim)
Show code cell source
# Plot
fig, axes = plt.subplots(1,2, figsize=(10,5))
for i in range(n_exp):
axes[i].plot(nrolls_v, X2_m[:,i], 'o')
axes[i].plot([nrolls_v[0], nrolls_v[-1]], 2*[X2_rej_lim], '--', color='red')
axes[i].grid()
axes[i].set_xlabel("n.rolls")
if ( i == 0 ): axes[i].set_ylabel("test statistics, $X^2$")
axes[i].set_title(f"Experiment: {name_l[i]}")
# Statistics about rejection rate
print(f"N. of rejections of H0, over {ntests} tests")
for i in range(n_exp):
str_false_positive = ' (false positive) ' if name_l[i] == 'Fair' else ''
print( (f"- Experiment: {name_l[i]:10.10s}, "
f"{rej_count[i]:5.0f}, " \
f"{rej_count[i]/ntests*100:4.1f}% {str_false_positive}") )
N. of rejections of H0, over 500 tests
- Experiment: Fair , 24, 4.8% (false positive)
- Experiment: Rigged , 493, 98.6%
18.2.1.4. Wilcoxon#
…todo
