17.1.2. Variabili casuali discrete#

17.1.2.1. Funzione di probabilità#

La funzione di probabilità, \(p_X(x)\), o funzione di massa, o densità di probabilità con un abuso per analogia con le variabili continue, è la funzione che associa la probabilità al valore \(x\) della variabile casuale \(X\). Data al variabile casuale \(X: \Omega \rightarrow E\), la proababilità del valore discreto \(x \in E\) è data dalla somma delle probabilità degli eventi disgiunti \(\Omega_x := \{ \omega \in \Omega \, | \, X(\omega) = x \}\) che producono il valore \(x\),

\[p_X(x) = \sum_{\omega_i \in \Omega_x} \nu(\omega_i) \ .\]

Proprietà.

  • \(p_X \ge 0\)

  • \(\sum_{x_k \in E} p_X(x_k) = 1\)

E da queste due proprietà segue che la probabilità del singolo valore è non superiore a 1, \(p(x_k) \le 1\).

17.1.2.2. Esempi di variabili discrete#

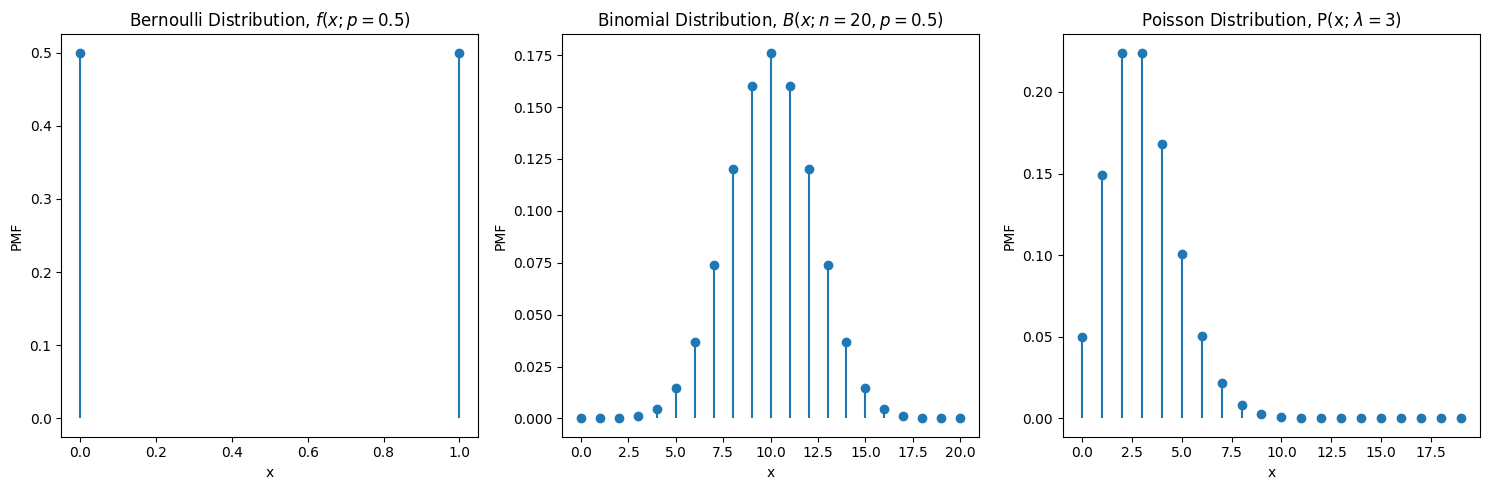
Si anticipano qui alcuni esempi di variabili casuali discrete, rapprestandone la loro distribuzione di probabilità: la distribuzione di Bernoulli, la distribuzione binomiale, e la distribuzione di Poisson. La distribuzione di Bernoulli può rappresentare la probabilità che il lancio di una moneta dia testa:\(0\) o croce:\(1\), la distribuzione binomiale può rappresentare la probabilità di ottenere \(x\) volte croce in \(n\) lanci; la distribuzione di Poisson viene usata per rappresentare eventi discreti rari, dei quali si conosce la media \(\lambda\).

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli, binom, poisson

# Define parameters for the distributions
p_bernoulli = 0.5                 # Probability for Bernoulli
n_binomial, p_binomial = 20, 0.5  # Number of trials and probability for Binomial
n_poisson, mu_poisson = 20, 3     # Mean for Poisson

# Create x values for the distributions
x_bernoulli = [0, 1]
x_binomial = np.arange(0, n_binomial + 1)
x_poisson = np.arange(0, n_binomial)  # Arbitrary range for Poisson

# Calculate the probabilities
y_bernoulli = bernoulli.pmf(x_bernoulli, p_bernoulli)
y_binomial = binom.pmf(x_binomial, n_binomial, p_binomial)
y_poisson = poisson.pmf(x_poisson, mu_poisson)

# Create subplots
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Plot Bernoulli
axes[0].stem(x_bernoulli, y_bernoulli, basefmt=" ", use_line_collection=True)
axes[0].set_title(f"Bernoulli Distribution, $f\\left(x; p={p_bernoulli} \\right)$")
axes[0].set_xlabel("x")
axes[0].set_ylabel("PMF")

# Plot Binomial
axes[1].stem(x_binomial, y_binomial, basefmt=" ", use_line_collection=True)
axes[1].set_title(f"Binomial Distribution, $B(x; n={n_binomial},p={p_bernoulli})$")
axes[1].set_xlabel("x")
axes[1].set_ylabel("PMF")

# Plot Poisson
axes[2].stem(x_poisson, y_poisson, basefmt=" ", use_line_collection=True)
axes[2].set_title(f"Poisson Distribution, P(x; $\\lambda={mu_poisson}$)")
axes[2].set_xlabel("x")
axes[2].set_ylabel("PMF")

# Adjust layout
plt.tight_layout()
plt.show()
../../_images/136305ea5229770747aff0206d802d1741ac2f86b63e9a3f3e88b2377b482e71.png
Hide code cell source 
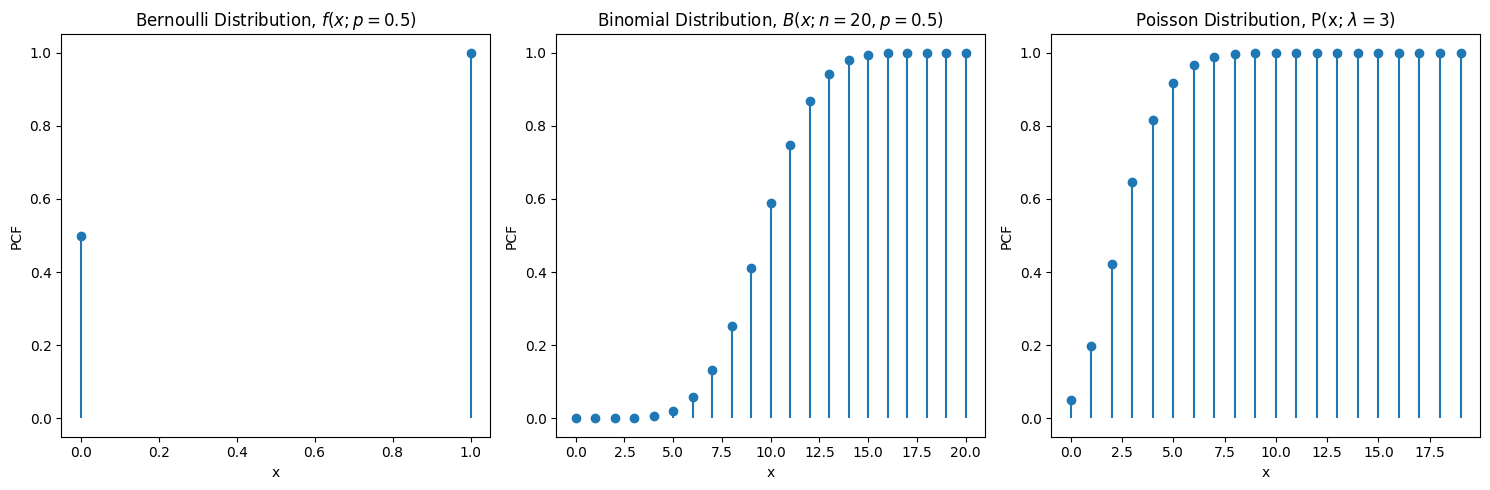
#> Cumulative function
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Plot Bernoulli
axes[0].stem(x_bernoulli, np.cumsum(y_bernoulli), basefmt=" ", use_line_collection=True)
axes[0].set_title(f"Bernoulli Distribution, $f\\left(x; p={p_bernoulli} \\right)$")
axes[0].set_xlabel("x")
axes[0].set_ylabel("PCF")

# Plot Binomial
axes[1].stem(x_binomial, np.cumsum(y_binomial), basefmt=" ", use_line_collection=True)
axes[1].set_title(f"Binomial Distribution, $B(x; n={n_binomial},p={p_bernoulli})$")
axes[1].set_xlabel("x")
axes[1].set_ylabel("PCF")

# Plot Poisson
axes[2].stem(x_poisson, np.cumsum(y_poisson), basefmt=" ", use_line_collection=True)
axes[2].set_title(f"Poisson Distribution, P(x; $\\lambda={mu_poisson}$)")
axes[2].set_xlabel("x")
axes[2].set_ylabel("PCF")

# Adjust layout
plt.tight_layout()
plt.show()
Hide code cell output
../../_images/5f1312c879583c1156187ed43ceb9c5d6a168c37be7bb6c94ef5a10d878d0ae4.png

17.1.2.3. Momenti#

Valore medio. Il valore medio di una variabile casuale è la media dei valori possibili \(x_k \in E\) pesata della probabilità \(p(x_k)\),

\[\begin{split}\begin{aligned} \mu_X = \text{E}[X] & := \sum_{x_k \in E} p(x_k) x_k = \\ & = \sum_{x_k \in E} \sum_{\omega_i \in \Omega_x} \nu(\omega_i) X(\omega_i) = \\ & = \sum_{\omega_i \in \Omega} \nu(\omega_i) X(\omega_i) \ . \end{aligned}\end{split}\]

equivalente alla media dei valori della variabile \(X(\omega_i)\) pesata sulle probabilità degli eventi \(\omega_i \in \Omega\). La media di una varaibile casuale \(X\) viene comunemente indicata con \(\mu_X\), e così verrà fatto in seguito per motivi di sintesi.

Varianza. La varianza è una misura della dispersione dei valori di una varaibile casuale attorno al suo valore medio, ed è definita come la media pesata degli scarti quadratici,

\[\sigma^2_X = E[(X-\mu_X)^2] = \sum_k p(x_k) (x_k - \mu_X)^2 \ .\]

Analogamente a quanto fatto per il valore medio, anche questa media può essere riferita sia ai valori sia agli eventi.

La variazione standard è definita come la radice quadra della varianza. A differenza della varianza, è una grandezza omogenea (!) alla variabile casuale: ad esempio, la media di una misura di lunghezza può essere \(2 \, m\) con deviazione standard \(0.1 \, m\), mentre la varianza è \(0.01 \, m^2\).

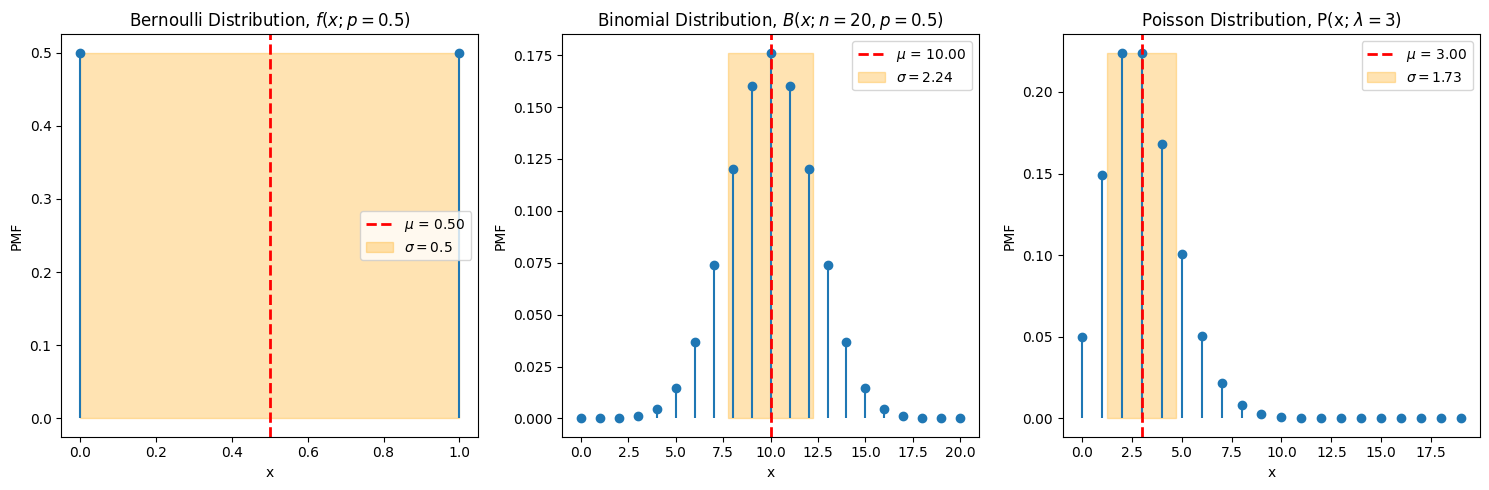
Di seguito vengono mostrati il valore medio e la deviazione standard - rappresentata qui come un intervallo centrato attorno alla media, anche se questa rappresentazione può essere ingannevole (!) per distribuzioni di probabilità non simmetriche - delle variabili casuali presentate in precedenza. In seguito, verrà introdotto il concetto di intervallo di confidenza. todo riferimento?

Oss. Nonostante siano rappresentati in tutto il grafico, si deve pensare alla media come un valore sull’asse \(x\) dei valori della variabile casuale, e la deviazione standard come un intervallo sullo stesso asse \(x\), ricordando le osservazioni fatte in precedenza sulla rappresentazione della deviazione standard.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli, binom, poisson

# Define parameters for the distributions
p_bernoulli = 0.5   # Probability for Bernoulli
n_binomial, p_binomial = 20, 0.5  # Trials and probability for Binomial
n_poisson, mu_poisson = 20, 3      # Mean for Poisson

# Create x values and calculate PMF for each distribution
x_bernoulli = [0, 1]
y_bernoulli = bernoulli.pmf(x_bernoulli, p_bernoulli)
mean_bernoulli, var_bernoulli = bernoulli.stats(p_bernoulli, moments='mv')

x_binomial = np.arange(0, n_binomial + 1)
y_binomial = binom.pmf(x_binomial, n_binomial, p_binomial)
mean_binomial, var_binomial = binom.stats(n_binomial, p_binomial, moments='mv')

x_poisson = np.arange(0, n_poisson)  # Arbitrary range for Poisson
y_poisson = poisson.pmf(x_poisson, mu_poisson)
mean_poisson, var_poisson = poisson.stats(mu_poisson, moments='mv')

# Set up the subplots
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Plot Bernoulli Distribution
axes[0].stem(x_bernoulli, y_bernoulli, basefmt=" ", use_line_collection=True)
axes[0].axvline(mean_bernoulli, color='red', linestyle='--', linewidth=2, label=f'$\mu$ = {mean_bernoulli:.2f}')
axes[0].fill_betweenx([0, max(y_bernoulli)], x1=mean_bernoulli - np.sqrt(var_bernoulli), x2=mean_bernoulli + np.sqrt(var_bernoulli), color='orange', alpha=0.3, label=f"$\sigma = {np.sqrt(var_bernoulli)}$")
axes[0].set_title(f"Bernoulli Distribution, $f\\left(x; p={p_bernoulli} \\right)$")
axes[0].set_xlabel("x")
axes[0].set_ylabel("PMF")
axes[0].legend()

# Plot Binomial Distribution
axes[1].stem(x_binomial, y_binomial, basefmt=" ", use_line_collection=True)
axes[1].axvline(mean_binomial, color='red', linestyle='--', linewidth=2, label=f'$\mu$ = {mean_binomial:.2f}')
axes[1].fill_betweenx([0, max(y_binomial)], x1=mean_binomial - np.sqrt(var_binomial), x2=mean_binomial + np.sqrt(var_binomial), color='orange', alpha=0.3, label=f"$\sigma = {np.sqrt(var_binomial):0.2f}$")
axes[1].set_title(f"Binomial Distribution, $B(x; n={n_binomial},p={p_bernoulli})$")
axes[1].set_xlabel("x")
axes[1].set_ylabel("PMF")
axes[1].legend()

# Plot Poisson Distribution
axes[2].stem(x_poisson, y_poisson, basefmt=" ", use_line_collection=True)
axes[2].axvline(mean_poisson, color='red', linestyle='--', linewidth=2, label=f'$\mu$ = {mean_poisson:.2f}')
axes[2].fill_betweenx([0, max(y_poisson)], x1=mean_poisson - np.sqrt(var_poisson), x2=mean_poisson + np.sqrt(var_poisson), color='orange', alpha=0.3, label=f"$\sigma = {np.sqrt(var_poisson):0.2f}$")
axes[2].set_title(f"Poisson Distribution, P(x; $\\lambda={mu_poisson}$)")
axes[2].set_xlabel("x")
axes[2].set_ylabel("PMF")
axes[2].legend()

# Adjust layout
plt.tight_layout()
plt.show()
../../_images/f7ed6c19b2a60b6d9381613feced82dc7fa26d4847689119ed6079dbd6baded8.png

17.1.2.4. Variabili casuali multi-dimensionali#

  • Probabilità congiunta. \(p(x,y)\)

  • Probabilità condizionale. \(p(x|y)\)

  • Probabilità marginale. \(p(x)\)

17.1.2.4.1. Probabilità congiunta e teorema di Bayes#

(17.1)#\[p(x,y) = p(x|y)p(y) = p(y|x)p(x)\]

17.1.2.4.2. Teorema di Bayes#

Dalla formula (17.1) della probabilità congiunta è immediato ricavare l’espressione del teorema di Bayes

\[p(y|x) = \frac{p(x|y)p(y)}{p(x)} \ .\]

17.1.2.4.3. Variabili indipendenti#

Due variabili casuali sono indipendenti se la probabilità condizionale di una variabile coincide con la sua probabilità marginale,

\[p(x|y) = p(x) \ ,\]

così che la probabilità congiunta di due variabili casuali indipendenti è il prodotto delle probabilità marginali,

\[p(x,y) = p(x)p(y) \ .\]

17.1.2.4.4. Covarianza#

\[\sigma^2_{ij} = E[(X_i-\mu_i)(X_j-\mu_j)] = R_{ij} - \mu_i \mu_j\]

17.1.2.4.5. Correlazione#

\[\rho_{XY} = \frac{E[(X-\mu_X)(Y-\mu_Y)]}{E[(X-\mu_X)^2]^{1/2} \, E[(X-\mu_X)^2]^{1/2}} = \frac{\sigma_{XY}^2}{\sigma_X \, \sigma_Y}\]