17.1.4. Trasformazione di probabilità di densità

17.1.4.1. Variabile singola

17.1.4.1.1. Cambio di variabile

17.1.4.1.1.1. Traslazione

Data la variabile casuale \(X\) con distribuzione di probabilità \(f_X(x)\) nota, la variabile casuale

\[Y = X + a\]

ha funzione di probabilità

\[f_Y(x+a) = f_X(x) \ .\]

Tra la media e la varianza delle due variabili casuali valgono le relazioni

\[\mu_Y = \mu_X + a \qquad , \qquad \sigma^2_Y = \sigma^2_X \ .\]

La dimostrazione è lasciata come esercizio.

Dimostrazione.

La probabilità che la variabile \(Y = X + a\) abbia valore \(y = x + a \in [ y_0, y_0 + dy ]\), è uguale alla probabilità che l’evento \(X\) abbia valore \(x \in [x_0, x_0 + dx]\), con \(x_0 = y_0 - a\) e \(dy = dx\),

\[\begin{split}\begin{aligned} P(Y \in [y_0, y_0 + dy]) & = P(X + a \in [y_0, y_0 + dy]) = \\ & = P(X \in [y_0 - a, y_0 - a + dy]) = \\ & = P(X \in [x_0, x_0 + dx]) \end{aligned}\end{split}\]

Per la definizione di densità di probabilità,

\[\begin{split}\begin{aligned} P(Y \in [y_0, y_0 + dy]) & = \int_{y=y_0}^{y_0 + dy} f_Y(y) \, dy = & y_0 = x_0 + a \\ & = \int_{y=x_0+a}^{x_0 + a + dx} f_Y(y) \, dy = & x = y - a, \ dy = dx \\ & = \int_{x=x_0}^{x_0+dx} f_Y(x-a) \, dx \\ P(X \in [x_0, x_0 + dx]) & = \int_{x=x_0}^{x_0+dx} f_X(x) \, dx \end{aligned}\end{split}\]

dal confronto tra i due termini, e dall’arbitrarietà di \(x_0\) e \(dx\), si ottiene \(f_{X}(x) = f_Y(x-a)\).

17.1.4.1.1.2. Scalatura

Data la variabile casuale \(X\) con distribuzione di probabilità \(f_X(x)\) nota, la variabile casuale

\[Y = \frac{X}{a}\]

ha funzione di probabilità

\[f_Y\left( \frac{x}{a} \right) = a f_X(x)\]

Tra la media e la varianza delle due variabili casuali valgono le relazioni

\[\mu_Y = \frac{\mu_X}{a} \qquad , \qquad \sigma^2_Y = \frac{\sigma^2_X}{a^2} \ .\]

La dimostrazione è lasciata come esercizio.

Dimostrazione.

La probabilità che la variabile \(Y = \frac{X}{a}\) abbia valore \(y = \frac{x}{a} \in [ y_0, y_0 + dy ]\), è uguale alla probabilità che l’evento \(X\) abbia valore \(x \in [x_0, x_0 + dx]\), con \(x_0 = a y_0\) e \(dy = a dx\),

\[\begin{split}\begin{aligned} P(Y \in [y_0, y_0 + dy]) & = P\left( \frac{X}{a} \in [y_0, y_0 + dy]\right) = \\ & = P(X \in [a y_0, a y_0 + a dy]) = \\ & = P(X \in [x_0, x_0 + dx]) \end{aligned}\end{split}\]

Per la definizione di densità di probabilità,

\[\begin{split}\begin{aligned} P(Y \in [y_0, y_0 + dy]) & = \int_{y=y_0}^{y_0 + dy} f_Y(y) \, dy = & y_0 = \frac{x_0}{a} \\ & = \int_{y=a \, x_0}^{a x_0 + a dx} f_Y(y) \, dy = & y = \frac{x}{a}, \ dy = \frac{dx}{a} \\ & = \frac{1}{a} \int_{x=x_0}^{x_0+dx} f_Y\left( \frac{x}{a} \right) \, dx \\ P(X \in [x_0, x_0 + dx]) & = \int_{x=x_0}^{x_0+dx} f_X(x) \, dx \end{aligned}\end{split}\]

dal confronto tra i due termini, e dall’arbitrarietà di \(x_0\) e \(dx\), si ottiene \(f_{X}(x) = \frac{1}{a} f_Y\left(\frac{x}{a}\right)\).

17.1.4.1.1.3. Trasformazione affine

Combinando la traslazione e la scalatura, si ottiene la più generale trasformazione affine

\[X = \frac{Y - y_0}{a} \ ,\]

usata spesso come scalatura delle variabili nel preprocessing. todo riferimento a scalatura di variabili su valori significativi del problema, per bilanciare il problema e lavorare con variabili non-dimensionali significatie con lo stesso ordine di grandezza (!!!)

Tra la media e la varianza delle due variabili casuali valgono le relazioni

\[\mu_X = \frac{\mu_Y - y_0}{a} \qquad , \qquad \sigma^2_X = \frac{\sigma^2_Y}{a^2} \ .\]

La dimostrazione è lasciata come esercizio.

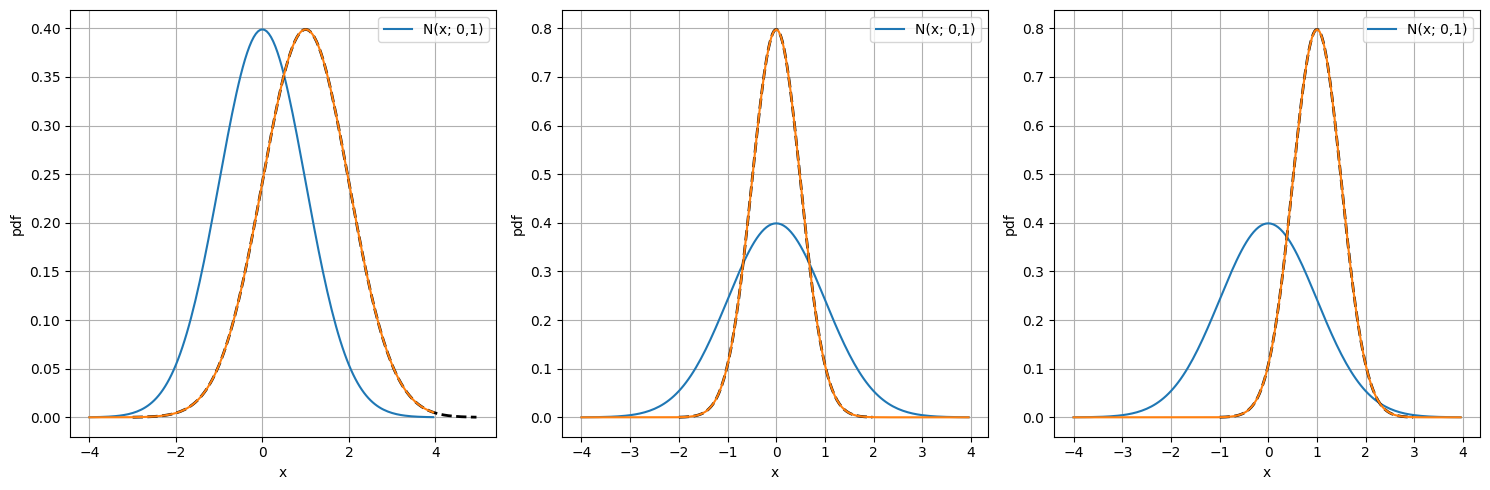
Le tre trasformazione discusse vengono applicate alla variabile normale \(X \sim N(x; \mu=0, \sigma^2=1)\). In particolare si mostrano gli effetti delle trasformazioni: 1. \(X = Y + 1\); 2. \(X = 2 Y\); 3. \(X = 2 (Y - 1)\)

Show code cell source Hide code cell source

%reset -f
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Define parameters for the distributions
mu, sigma = 0., 1.                # Property of Gaussian
a_transl, a_scale  = 1., 2.

transl_v = np.array([ a_transl, 0., a_transl ])
scale_v  = np.array([ 1., a_scale, a_scale ])
mu_v = mu + transl_v
sigma_v = sigma / scale_v

# Create x values for the distributions
x0_plot = np.arange(-4.,4., .05)
p0_norm = norm.pdf(x0_plot, loc=mu, scale=sigma)

xv_plot, pv_norm = [], []
for i in range(len(transl_v)):
    xv_plot += [ x0_plot / scale_v[i] + transl_v[i] ]
    pv_norm += [ norm.pdf(x0_plot, loc=mu_v[i], scale=sigma_v[i]) ]
    
# Create subplots
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Plot
for i in range(len(transl_v)):
    axes[i].plot(x0_plot, p0_norm, label="N(x; 0,1)") #
    axes[i].plot(xv_plot[i], p0_norm*scale_v[i], '--', color='black', lw=2)
    axes[i].plot(x0_plot, pv_norm[i])
    axes[i].set_xlabel("x")
    axes[i].set_ylabel("pdf")
    axes[i].grid()
    axes[i].legend()

# Adjust layout
plt.tight_layout()
plt.show()

17.1.4.2. Multi-variabile

17.1.4.2.1. Cambio di variabili

17.1.4.2.2. Combinazione di variabili

17.1.4.2.2.1. Somma

Date due variabili casuali \(X\), \(Y\), con probabilità congiunta \(p_{XY}(x,y)\), la loro somma \(Z = X + Y\) è una variabile casuale dipendente con distribuzione di probabilità

\[p(z) = \int_y p_{XY}(z-y,y) \, dy = \int_{x} p_{XY}(x, z-x) \, dx \ .\]

Se le due variabili sono tra di loro statisticamente indipendenti, la densità di probabilità congiunta è uguale al prodotto delle densità di probabilità delle singole variabili, \(p_{XY}(x,y) = p_X(x) p_Y(y)\), e quindi la densità di probabilità della somma è uguale alla convoluzione tra le densità di probabilità delle due variabili,

\[p(z) = \int_y p_{X}(z-y) \, p_{Y}(y) \, dy \ .\]

Valore atteso

Il valore atteso della somma è quindi

\[E[Z] = \int_z z \, p(z) \, dz = \int_{y,z} z \, p_{XY}(z-y,y) \, dy \, dz = \int_{x,y} (x+y) \, p_{XY}(x,y) \, dx \, dy \ , \]

e, nel caso in cui le due variabili siano tra di loro statisticamente indipendenti,

\[\begin{split}\begin{aligned} E[Z] & = \int_{x,y} (x + y) \, p_X(x) \, p_Y(y) \, dx \, dy = \\ & = \int_{x,y} x \, p_X(x) \, p_Y(y) \, dx \, dy + \int_{x,y} y \, p_X(x) \, p_Y(y) \, dx \, dy = \\ & = \int_x x \, p_X(x) \, dx + \int_y y \, p_Y(y) \, dy = E[X] + E[Y] \ . \end{aligned}\end{split}\]

Varianza

La varianza della somma è

\[\begin{aligned} \sigma_Z^2 = E\left[(Z - E[Z])^2\right] = E\left[Z^2\right] - E[Z]^2 = \int_z z^2 p(z) \, dz - E[Z]^2 \end{aligned}\]

e nel caso le due variabili siano tra di loro statisticamente indipendenti,

\[\begin{split}\begin{aligned} \sigma_Z^2 & = \int_z z^2 p(z) \, dz - E[Z]^2 = \\ & = \int_{x,y} (x+y)^2 \, p_{X}(x) \, p_{Y}(y) \, dx \, dy - \left(E[X] + E[Y]\right)^2 = \\ & = \int_{x} x^2 \, p{X}(x) \, dx + \int_{y} y^2 \, p_Y(y) \, dy + 2 E[X] E[Y] - \left( E[X]^2 + 2 E[X] E[Y] + E[Y]^2 \right) = \\ & = \int_{x} x^2 \, p{X}(x) \, dx - E[X]^2 + \int_{y} y^2 \, p_Y(y) \, dy - E[Y]^2 = \\ & = \sigma_X^2 + \sigma_Y^2 \ . \end{aligned}\end{split}\]

17.1.4.2.2.2. Prodotto

Date due variabili casuali \(X\), \(Y\) con probabilità congiunta \(p_{XY}(x,y)\), il loro prodotto \(Z = X \cdot Y\) è una variabile casuale dipendente con distribuzione di probabilità

\[p(z) = \int_{y} p_{XY} \left(\frac{z}{y}, y \right) \, dy = \int_{x} p_{XY} \left(x, \frac{z}{x} \right) \, dx\]

Se le due variabili sono statisticamente indipendenti

\[p(z) = \int_x p_X(x) \, p_Y\left( \frac{z}{x} \right) \, dx\]

(todo ha qualche uso questa formula? Si ritrova la convoluzione con il cambio di variabili \(z=e^v\), \(x=e^u\))

Valore atteso

Il valore atteso del prodotto è

\[E[Z] = \int_z z \, p(z) \, dz = \int_{y,z} z \, p_{XY}\left(\frac{z}{y},y\right) \, dy \, dz = \int_{x,y} x y \, p_{XY}(x,y) \, dx \, dy \ , \]

e, nel caso in cui le due variabili siano tra di loro statisticamente indipendenti,

\[\begin{split}\begin{aligned} E[Z] & = \int_{x,y} x y \, p_X(x) \, p_Y(y) \, dx \, dy = \\ & = \int_{x} x \, p_X(x) \, dx \cdot \int_y y \, p_Y(y) \, dy = E[X] \cdot E[Y] \ . \end{aligned}\end{split}\]

Varianza

La varianza del prodotto è

\[\begin{aligned} \sigma_Z^2 = ... \end{aligned}\]

e nel caso le due variabili siano tra di loro statisticamente indipendenti,

\[\begin{split}\begin{aligned} \sigma_Z^2 & = \int_{x,y} x^2 y^2 p_X(x) \, p_Y(y) \, dx \, dy - \left( E[X] \, E[Y] \right)^2 = \\ & = R_X^2 \, R_Y^2 - E[X]^2 \, E[Y]^2 = \\ & = \left( \sigma_X^2 + E[X]^2 \right)\left( \sigma_Y^2 + E[Y]^2 \right) - E[X]^2 \, E[Y]^2 = \\ & = \sigma_X^2 \, \sigma_Y^2 + \sigma_X^2 \, E[Y]^2 + \sigma_Y^2 \, E[X]^2 \end{aligned}\end{split}\]

In termini di correlazione, \(R_X^2 = \sigma_X^2 + E[X]^2\),

\[R_Z^2 = R_X^2 \, R_Y^2 \ .\]