18.2.4.4. t-test#

Un t-test è un test di verifica delle ipotesi nel quale la statistica test ha una distribuzione t di Student sotto l’ipotesi nulla H0,

p(x|H0)∼tν

18.2.4.4.1. t-test per un campione#

Il t-test per un campione è un test di verifica del valore di un parametro, per la media di una variabile casuale sotto un’opportuna ipotesi nulla H0. Il parametro t,

t=x^−μ0s^n ,

confronta la distanza della media x¯ del campione dal valore medio μ0 della distribuzione p(x|H0), con la deviazione standard del campione s opportunamente scalata della grandezza del campione n.

Se le osservazioni della variabile casuale sono indipdendenti tra di loro, allora t è una variabile casuale che tende a una variabile normale N(0,1) per il teorema del limite centrale todo link a una sezione sul campionamento

# Example

import numpy as np
from scipy.stats import ttest_1samp, t

import matplotlib.pyplot as plt

# Test statistics has expected value mu0 under H0 hypotesis
mu0 = 86.          # Expeceted value of the test statistics under H0
sigma = 0.05       # Significance level


# Sample data: test scores from two classes
sample = [88, 92, 85, 91, 87]
n_s = len(sample)
mu_s = np.sum(sample)/n_s
s_s = ( np.sum((sample-mu_s)**2)/(n_s-1) )**.5

print("Sample statistics:")
print(f" sample avg    : {mu_s}")
print(f" sample std.dev: {s_s}")


# Perform independent t-test
t_statistic, p_value = ttest_1samp(sample, mu0)

print(f"\n1-sample t-test")
print(f" t-Statistic: {t_statistic}")
print(f" p-Value    : {p_value}")


# Interpretation
if p_value < sigma:
    print("\n> Reject the null hypothesis, H0: the means of the two classes are significantly different.")
else:
    print("\n> Fail to reject the null hypothesis, H0: no significant difference in means between the classes.")

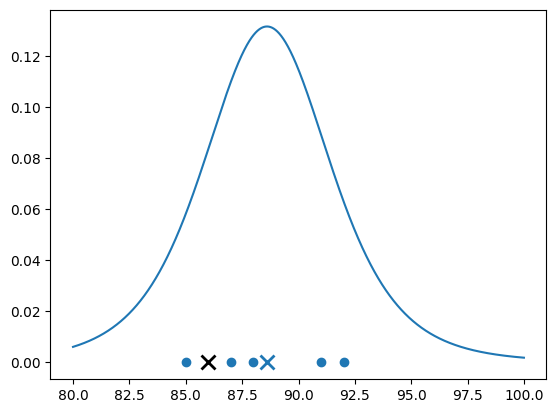
x_plot = np.arange(80, 100, .01)
t_pdf_plot = t.pdf(x_plot, n_s, mu_s, s_s)

plt.figure()
plt.plot(x_plot, t_pdf_plot, color=plt.cm.tab10(0))
plt.plot(sample, np.zeros(n_s), 'o', color=plt.cm.tab10(0))
plt.plot(mu_s, 0., 'x', color=plt.cm.tab10(0), markersize=10, markeredgewidth=2)
plt.plot(mu0 , 0., 'x', color='black'        , markersize=10, markeredgewidth=2)

Sample statistics:
 sample avg    : 88.6
 sample std.dev: 2.8809720581775866

1-sample t-test
 t-Statistic: 2.017991366836461
 p-Value    : 0.11375780482862627

> Fail to reject the null hypothesis, H0: no significant difference in means between the classes.

[<matplotlib.lines.Line2D at 0x7f9b30befa60>]
../../_images/b447209d18774c554d77059adc27f1afcb900a0a10e8e9db17f5ca0f6304b8c4.png

18.2.4.4.2. t-test per due campioni#

  • test con varianza uguale (o simile), t-test/test con varianza diversa, Welch

  • campioni indipendenti/campioni dipendenti (paired samples)

18.2.4.4.2.1. t-test per due variabili indipendenti, con varianza simile e stesso numero di osservazioni#

Nell’ipotesi che i campioni siano ottenuti da due variabili indipendenti, i risultati ottenuti nella sezione sulla combinazione di variabili casuali

  • il valore atteso della somma/differenza di variabili casuali indipendenti è uguale alla somma/differenza dei valori attesi delle singole variabili

  • la varianza della somma/differenza di variabili casuali indipendenti è uguale alla somma delle varianze delle singole variabili.

Il t-test per due campioni equivale al t-test per un campione uguale alla differenza delle osservazioni nei due campioni,

zi=xi−yi .
# Example

import numpy as np
from scipy.stats import ttest_ind

# Significance level
sigma = 0.05

# Sample data: test scores from two classes
class_A = [88, 92, 85, 91, 87]
class_B = [78, 85, 80, 83, 79]

nA = len(class_A); mu_A = np.sum(class_A)/nA; sA = ( np.sum((class_A-mu_A)**2)/(nA-1) )**.5
nB = len(class_B); mu_B = np.sum(class_B)/nB; sB = ( np.sum((class_B-mu_B)**2)/(nB-1) )**.5

print("Sample statistics:")
print("Sample A")
print(f" sample avg    : {mu_A}")
print(f" sample std.dev: {sA}")
print("Sample B")
print(f" sample avg    : {mu_B}")
print(f" sample std.dev: {sB}")


# Perform independent t-test
t_statistic, p_value = ttest_ind(class_A, class_B)


print(f"\ns-sample t-test")
print(f" t-Statistic: {t_statistic}")
print(f" p-Value    : {p_value}")

print((mu_A-mu_B)/((sA**2 + sB**2)/nA)**.5)

# Interpretation
if p_value < sigma:
    print("\nReject the null hypothesis: The means of the two classes are significantly different.")
else:
    print("\nFail to reject the null hypothesis: No significant difference in means between the classes.")

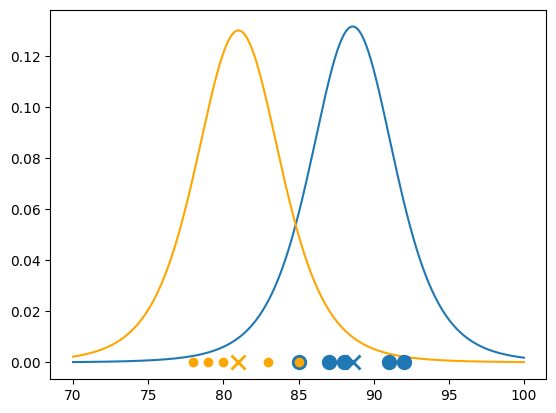
x_plot = np.arange(70, 100, .01)
t_pdf_A = t.pdf(x_plot, nA, mu_A, sA)
t_pdf_B = t.pdf(x_plot, nB, mu_B, sB)

plt.figure()
plt.plot(x_plot, t_pdf_A, color=plt.cm.tab10(0))
plt.plot(x_plot, t_pdf_B, color='orange')
plt.plot(class_A, np.zeros(nA), 'o', color=plt.cm.tab10(0), markersize=10)
plt.plot(class_B, np.zeros(nB), 'o', color='orange'       )
plt.plot(mu_A, 0., 'x', color=plt.cm.tab10(0), markersize=10, markeredgewidth=2)
plt.plot(mu_B, 0., 'x', color='orange'       , markersize=10, markeredgewidth=2)

Sample statistics:
Sample A
 sample avg    : 88.6
 sample std.dev: 2.8809720581775866
Sample B
 sample avg    : 81.0
 sample std.dev: 2.9154759474226504

s-sample t-test
 t-Statistic: 4.146139914483853
 p-Value    : 0.0032260379191180397
4.146139914483853

Reject the null hypothesis: The means of the two classes are significantly different.

[<matplotlib.lines.Line2D at 0x7f9b30b0ff70>]
../../_images/ad9e0a740f0f409ab9699cc4cac6809aff9c408ab244bacfcd1a9c9e8e4c1ab3.png 
#