18.2.2. Test di correlazione#
Test più comuni
regressione lineare
correlazione di Pearson
correlazione di Spearman
18.2.2.1. Regressione lineare#
regressione lineare
regressione lineare generalizzata
…
18.2.2.1.1. Metodo dei minimi quadrati per una regressione lineare#
Dati due campioni accoppiati \(\{X_n\}_{n=1:N}\), \(\{Y_n\}_{n=1:N}\) campionati dalle popolazioni \(X\), \(Y\), si calcolano i coefficienti \(\symbf{\theta} = (a, b)\) dell’approssimazione lineare \(y(x|\theta) = a x + b\) che rendono minimo l’errore quadratico medio
La funzione è quadratica in \(a\), \(b\) e semi-definita positiva. Si cercano i valori che rendono minimo l’errore ponendo uguale a \(0\) le derivate parziali dell’errore rispetto ai parametri
Queste due equazioni formano un sistema lineare di due equazioni in due incognite, che può essere riscritto con il formalismo matriciale
Il valore dei coefficienti ottimi \(\theta^* = (a, b)\) che minimizzano l’errore quadratico medio si trova come soluzione del sistema lineare, l’errore quadratico medio minimo dovuto all’approssimazione viene calcolato in seguito, \(e(\theta^*)\). La bontà dell’approssimazione lineare può essere valutata in termini dell’errore quadratico medio.
Regressione e SL. Una delle applicazioni fondamentali in ML, in particolare in SL, è la regressione o l’approssimazione di funzioni; scelta del modello…
18.2.2.1.2. Metodo ed errore#
Il sistema lineare può essere riscritto come
e la soluzione
L’errore minimo diventa quindi
18.2.2.2. Correlazione di Pearson#
Il coefficiente di correlazione tra due variabili casuali \(X\), \(Y\) è definito come il rapporto tra la loro covarianza e il prodotto delle loro deviazioni standard,
Coefficiente di correlazione per campioni. Usando le statistiche campionarie per i campioni a disposizione delle due popolazioni,
Coefficiente di correlazione in statistica inferenziale. I metodi di statistica basati sul coefficiente di correlazione di Pearson hanno due obiettivi:
valutare l’ipotesi nulla \(\text{H}_0\) che afferma che l’assenza di correlazione tra le due popolazioni, \(\rho = 0\), sulla base del valore del coefficiente \(r\) calcolato sui campioni
fornire un intervallo di confidenza che contenga \(\rho\)
Alcuni metodi per ottenere questi due obiettivi sono:
permutazione
bootstrap
errore standard, assumendo una relazione lineare tra \(x\) e \(y\), con l’aggiunta di un errore gaussiano \(\varepsilon\), \(y = a x + b + \varepsilon\), \(\sigma_r = \sqrt{\frac{1-r^2}{n-2}}\)
\(t\)-test sulla variabile \(t = \frac{r}{\sigma_r}\)
…
18.2.2.3. Correlazione di Spearman#
per ranghi
per relazioni non lineari ma monotone … todo
18.2.2.4. Esempio#
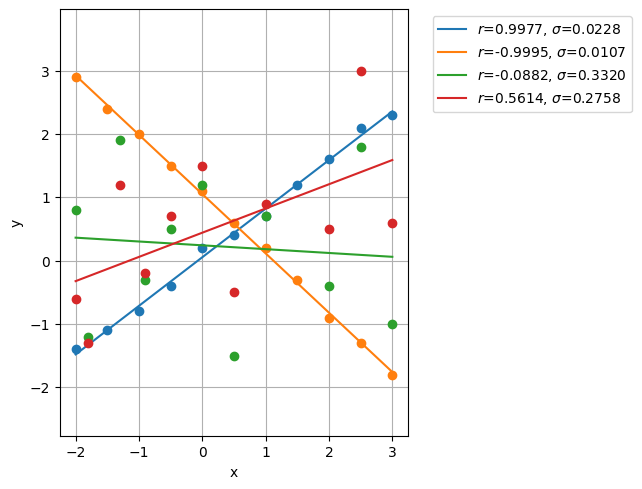
Si valutano i metodi di correlazione per 4 coppie di campioni, 2 che mostrano una buona correlazione e 2 con correlazione scarsa
Show code cell source
# Test correlation algorithms
import numpy as np
import matplotlib.pyplot as plt
#> Data
pairs = [
{ # Good Positive Correlation
'x': np.array([-2.0, -1.5, -1.0, -0.5, 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0]),
'y': np.array([-1.4, -1.1, -0.8, -0.4, 0.2, 0.4, 0.7, 1.2, 1.6, 2.1, 2.3])
},
{ # Good Negative Correlation
'x': np.array([-2.0, -1.5, -1.0, -0.5, 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0]),
'y': np.array([2.9, 2.4, 2.0, 1.5, 1.1, 0.6, 0.2, -0.3, -0.9, -1.3, -1.8])
},
{ # Bad Correlation
'x': np.array([-2.0, -1.8, -1.3, -0.9, -0.5, 0.0, 0.5, 1.0, 2.0, 2.5, 3.0]),
'y': np.array([0.8, -1.2, 1.9, -0.3, 0.5, 1.2, -1.5, 0.7, -0.4, 1.8, -1.0])
},
{ # Bad Correlation
'x': np.array([-2.0, -1.8, -1.3, -0.9, -0.5, 0.0, 0.5, 1.0, 2.0, 2.5, 3.0]),
'y': np.array([-.6, -1.3, 1.2, -0.2, 0.7, 1.5, -0.5, 0.9, 0.5, 3.0, 0.6])
}
]
# plt.figure()
# for i in range(len(pairs)):
# plt.plot(pairs[i]['x'], pairs[i]['y'], 'o', color=plt.cm.tab10(i))
# plt.grid()
# plt.axis('equal')
Show code cell source
plt.figure()
for i in range(len(pairs)):
#> Scale and normalize data
x, y = pairs[i]['x'], pairs[i]['y']
n = len(pairs[i]['x'])
# ...
x_mean = np.mean(x)
y_mean = np.mean(y)
nSxy = np.sum( (x-x_mean) * (y-y_mean) )
nSx2 = np.sum( (x-x_mean)**2 )
nSy2 = np.sum( (y-y_mean)**2 )
#> LS linear system
A = np.array([ [ np.sum(x**2) , np.sum(x)], [ np.sum(x), n ] ] ) / n
f = np.array([ np.sum(x * y) , np.sum(y) ]) / n
#> Find coefficients of the regression
z = np.linalg.solve(A, f)
#> Find average square error
e = np.sum( ( z[0]*x + z[1] - y )**2 ) / n
#> Pearson
#> correlation coefficient
r = nSxy / np.sqrt( nSx2 * nSy2 )
#> sigma
sigma = np.sqrt( (1 - r**2) / ( n-2 ) )
print(f"> Pair {i}")
print(f" Regression coeffs y = {z[0]:.4f} x + {z[1]:.4f}, with error {e**.5:.4f}")
print(f" Pearson correlation: {r:.4f}, sigma: {sigma:.4f}")
plt.plot(x, y , 'o', color=plt.cm.tab10(i))
plt.plot(x, z[0]*x+z[1], '-', color=plt.cm.tab10(i), label=f"$r$={r:.4f}, $\sigma$={sigma:.4f}")
plt.grid()
plt.legend(loc="upper left", bbox_to_anchor=(1.05, 1.0))
plt.tight_layout()
plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y')
> Pair 0
Regression coeffs y = 0.7673 x + 0.0527, with error 0.0831
Pearson correlation: 0.9977, sigma: 0.0228
> Pair 1
Regression coeffs y = -0.9364 x + 1.0500, with error 0.0477
Pearson correlation: -0.9995, sigma: 0.0107
> Pair 2
Regression coeffs y = -0.0604 x + 0.2410, with error 1.1254
Pearson correlation: -0.0882, sigma: 0.3320
> Pair 3
Regression coeffs y = 0.3824 x + 0.4404, with error 0.9296
Pearson correlation: 0.5614, sigma: 0.2758
Text(44.222222222222214, 0.5, 'y')