11.4.3. Three-phase electrical circuits in harmonic regime

Guidelines for solution

Analyse the network as a standard configuration of a three-phase network (star-star,…) and rely on results derived for three-phase circuits.

As an example, for a star-star configuration:

1. evaluate load impedances, impedances in parallel with the generators, interconnections between phases

2. evaluate voltage difference across the centers of the stars, \(v_{AB}\)

3. once \(v_{AB}\) is known, it should be easier to evaluate currents and voltages in the grid with KCL and KVL

4. use relations of power in harmonic regime, to answer the questions about power: just remember the difference between maximum and effective values, and that a wattmeter measures the active power

Exercise 11.11 (Exam 2024-09-06, Exercise 3.)

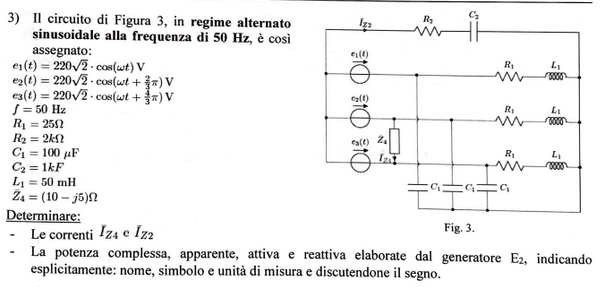
Solution

This network is a star-star connection with impedances

\[\begin{split}\begin{aligned} Z_g & = ( R_1 + s L_1 ) \parallel \frac{1}{s C_1} \qquad g = 1:3 \\ Z_4 & = R_2 + \frac{1}{s C_2} \end{aligned}\end{split}\]

and inter-connection between phases \(2\) and \(3\) with impedance \(Z_4\).

Voltage \(v_{AB}\).

\[v_{AB} = \dfrac{ \sum_{g=1}^{3} Y_g \, e_g }{\sum_{k=1}^{4} Y_4}\]

Generation and loads are equilibrated, and thus \(\sum_{g=1}^{3} Y_g \, e_g = 0\), and \(v_{AB} = 0\).

Current \(i_{Z_2}\). As \(v_{AB}=0\), then \(i_{Z_2} = 0\), as in general it whould be \(i_{Z_2} = \frac{v_{AB}}{R_2 + \frac{1}{sC_2}}\).

Current \(i_{Z_4}\). With KVL on the loop with the two tension generators \(e_2\), \(e_3\) closed with \(Z_4\)

\[\begin{split}\begin{aligned} 0 & = e_3 + Z_4 i_{Z_4} - e_2 \\ \rightarrow \quad i_{Z_4} & = \frac{e_2 - e_3}{Z_4} \end{aligned}\end{split}\]

Currents \(i_{e_2}\). Current \(i_{e_2}\) through the generator are evaluated through KVL between the centers of the stars,

\[\begin{split}\begin{aligned} 0 & = e_2 - \dfrac{1}{\frac{1}{R_1 + s L_1} + s C_1 } i_{e_2} - v_{AB} \\ \rightarrow \quad i_{e_2} & = \left[ \frac{1}{R_1 + s L_1} + s C_1 \right] e_2 \\ \end{aligned}\end{split}\]

Powers of generator \(2\).

\[\begin{split}\begin{aligned} S_2 & = V_2 I_2^* \\ A_2 & = |S_2| \\ P_2 & = \text{re} \{ S_2 \} \\ Q_2 & = \text{im} \{ S_2 \} \ , \end{aligned}\end{split}\]

using the effective values of tension and current \(V_2\), \(I_2\).

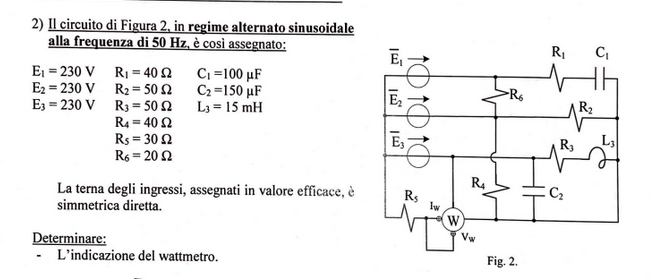
Exercise 11.12 (Exam 2024-07-22, Exercise 3.)

Solution

This network is a star-star connection with impedances

\[\begin{split}\begin{aligned} Z_1 & = ( R_1 + j X_{C_1} ) \parallel R_2 \\ Z_2 & = 0 \\ Z_3 & = ( R_3 + j X_{L_2} ) \parallel j X_{L_1} \\ Z_4 & = j X_{C_2} \end{aligned}\end{split}\]

and inter-connection between phase \(3\) and the netural with resistance \(R_4\), before \(Z_4\), and thus in parallel with the generator \(3\).

Voltage \(v_{AB}\). As \(Z_2 = 0\), it’s not possible to directly use

\[v_{AB} = \dfrac{ \sum_{g=1}^{3} Y_g \, e_g }{\sum_{k=1}^{4} Y_4} \ ,\]

or this must be used with the limit \(Y_2 \rightarrow + \infty\), and thus

\[v_{AB} = e_2 \ .\]

Wattmeter tension \(v_W\). KVL with the generators \(2\) and \(3\),

\[v_W = e_2 - e_3 \ .\]

Wattmeter current \(i_w = i_{e_2}\). KCL on the center of generation star, \(0 = i_{e_1} + i_{e_2} + i_{3} + i_{4}\), with

\[\begin{split}\begin{aligned} i_{e_1} & = \frac{1}{Z_1} ( e_1 - v_{AB} ) \\ i_{3} & = \frac{1}{Z_3} ( e_3 - v_{AB} ) \\ i_{4} & = -\frac{1}{Z_4} v_{AB} \ , \end{aligned}\end{split}\]

being \(i_3 = i_{e_3} + i_{R_4}\) the sum of the current in the parallel connection on the branch \(3\) of the generation. Thus, current \(i_{e_2}\) reads

\[\begin{split}\begin{aligned} i_{e_2} & = - i_{e_1} - i_{3} - i_{4} = \\ & = - \frac{e_1}{Z_1} - \frac{e_3}{Z_3} + \left( \frac{1}{Z_1} + \frac{1}{Z_3} + \frac{1}{Z_4} \right) v_{AB} \end{aligned}\end{split}\]

Wattmeter. Wattmeter reading provides the active power

\[P_w = \text{re} \{ S_w \} = \text{re} \{ v_w i_w^* \} \ .\]

Power on \(C_2\). Current and voltage across \(C_2\) are

\[\begin{split}\begin{aligned} i_{C_2} & = i_4 \\ v_{C_2} & = Z_{C_2} i_{C_2} = \frac{1}{s C_2} i_{C_2} \ , \end{aligned}\end{split}\]

and the complex power is

\[s = V_{C_2} I_{C_2}^* \ .\]

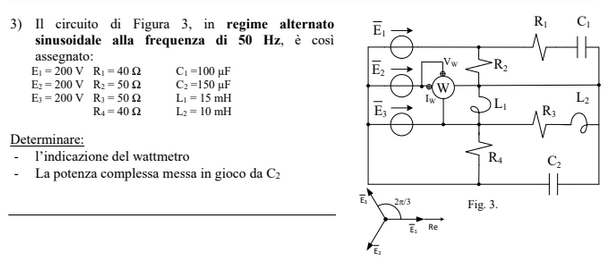
Exercise 11.13 (Exam 2024-06-19, Exercise 1.)

Solution

This network is a star-star connection with impedances

\[\begin{split}\begin{aligned} Z_1 & = ( R_2 + j X_{L_2} ) \parallel ( j X_{C_1} ) \\ Z_2 & = ( R_1 \parallel 0 ) \\ Z_3 & = ( R_3 + j X_{C_2} ) \parallel j X_{L_1} \\ \end{aligned}\end{split}\]

with \(L_2\) and \(R_4\) in parallel with generator \(e_2\). As \(R_1\) is in parallel with a short-circuit in \(Z_2\), this impedance is zero and as it is the current through \(R_1\). There’s no neutral.

Voltage \(v_{AB}\). As \(Z_2 = 0\) (see previous exercise), the voltage between the centers of the stars is

\[v_{AB} = e_2 \ .\]

Wattmeter tension \(v_W\). KVL with the generators \(2\) and \(3\),

\[v_W = e_1 - e_3 \ .\]

Wattmeter current \(i_w = i_{2}\). KCL on the center of generation star, \(0 = i_{e_1} + i_{2} + i_{e_3}\), with

\[\begin{split}\begin{aligned} i_{e_1} & = \frac{1}{Z_1} ( e_1 - e_2 ) \\ i_{e_3} & = \frac{1}{Z_3} ( e_3 - e_2 ) \\ \end{aligned}\end{split}\]

being \(i_2 = i_{e_2} + i_{L_1} + i_{R_4}\) the sum of the current in the parallel connection on the branch \(2\) of the generation. Thus, current \(i_{w}\) reads

\[\begin{split}\begin{aligned} i_w = i_{2} & = - i_{e_1} - i_{e_3} = \\ & = \frac{1}{Z_1} ( e_2 - e_1 ) + \frac{1}{Z_3} ( e_2 - e_3 ) \\ \end{aligned}\end{split}\]

Wattmeter. Wattmeter reading provides the active power

\[P_w = \text{re} \{ S_w \} = \text{re} \{ v_w i_w^* \} \ .\]

Power of tension generator \(e_1\).

\[s_{e_1} = e_{2} i_{e_2}^* \ .\]

…

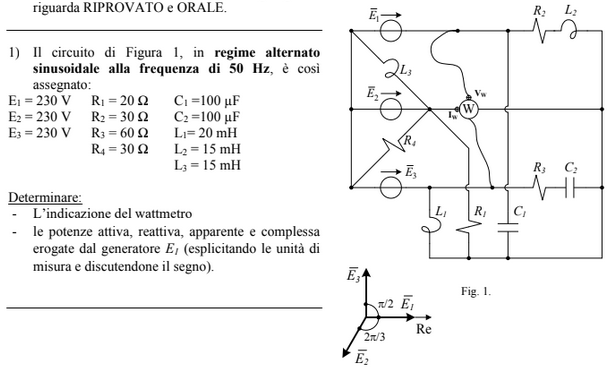
Exercise 11.14 (Exam 2024-02-13, Exercise 2.)

Solution - todo